Что такое цикл в графе?
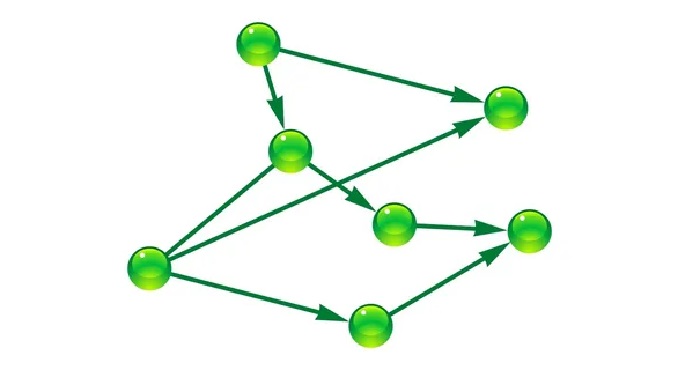
Цикл в графе — это последовательность рёбер и вершин, где первая вершина совпадает с последней, а все остальные вершины и рёбра различны. Граф называется цикличным, если в нём существует хотя бы один цикл.
Пример:
- Вершины: A, B, C
- Рёбра: (A,B), (B,C), (C,A)
В этом случае цикл — это путь A→B→C→A, потому что мы возвращаемся в исходную вершину A.
Есть два типа графов:
- Ориентированный граф (направленный граф): рёбра имеют направление. Цикл в ориентированном графе — это путь, где все рёбра идут в одном направлении.
- Неориентированный граф (ненаправленный граф): рёбра не имеют направления. Цикл в неориентированном графе — это путь, который возвращается в исходную вершину, но направление рёбер не имеет значения.
Цикл в графе важен для многих задач, таких как поиск маршрутов, определение связности графа, а также для нахождения проблемных областей в сетях.
Вот пример для неориентированного графа:
Предположим, есть 4 вершины: A, B, C, D и рёбра между ними:
- (A, B)
- (B, C)
- (C, A)
Тогда путь A→B→C→A образует цикл. Этот путь начинается и заканчивается в одной и той же вершине (A), а все рёбра и вершины (кроме начальной и конечной) уникальны.
Визуально это можно представить так:
A -- B
| |
C -- D
Здесь видно, что можно пройти по рёбрам A→B→C→A, образуя цикл.
Для ориентированного графа представим 3 вершины: X, Y, Z и рёбра между ними с направлением:
- X→Y
- Y→Z
- Z→X
Здесь тоже образуется цикл X→Y→Z→X, так как мы снова возвращаемся в вершину X.
Визуально:
X → Y
↑ ↓
Z ←
Этот цикл в ориентированном графе имеет чётко определённое направление, и мы движемся по рёбрам строго в указанном порядке.