Удивительно простая фигура решает давнюю математическую проблему

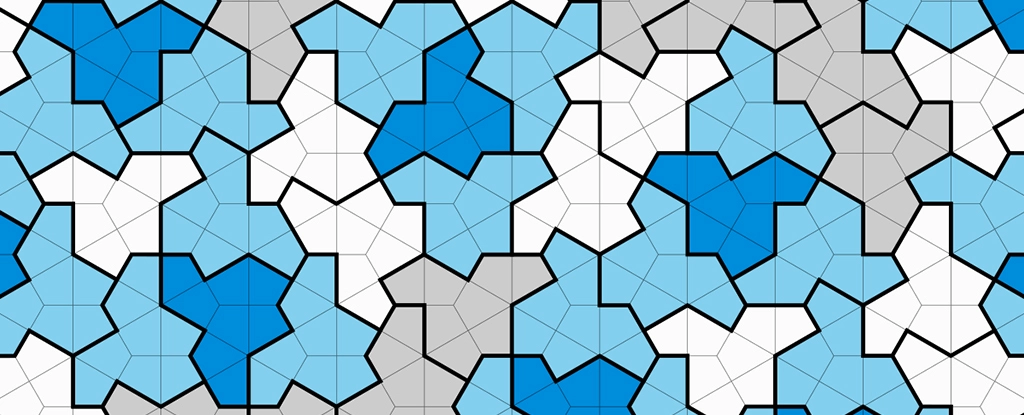
Группа математиков представила совершенно новую 13-гранную фигуру, которую они назвали «шляпой» (hat). Эту фигуру (немного похожая на фетровую шляпу) можно выкладывать как плитку на плоскости, создавая узоры, которые никогда не повторяются.

Подобные формы известны как апериодические моноплитки (мозаики).

«Апериодические наборы плиток проходят тонкую грань между порядком и беспорядком, допуская мозаику, но только без какой-либо трансляционной симметрии, никогда не допуская простого повторения периодической мозаики», — пишут ученые в своей статье.

Самый первый апериодический набор плиток был обнаружен в 1966 году и состоял из 20 426 форм. С годами это число уменьшилось, и сейчас существует несколько апериодических наборов плиток, состоящих всего из двух форм.

Однако до сих пор никто не придумал ни одной плитки, которая соответствовала бы критериям. Это то, что многие математики искали с 1960-х годов, что дает представление о важности этого открытия.

Когда вы смотрите на фигуру, она кажется настолько простой, что ее можно было бы найти несколько десятилетий назад — и действительно, сами исследователи называют ее «почти обыденной в своей простоте».

Ученые также представили новый метод доказательства существования будущих фигур, в котором различные изменения формы комбинируются, чтобы помочь установить, что они могут существовать вечно, не становясь симметричными в своих узорах.

Еще неизвестно, как «шляпа» будет использоваться исследователями, математиками и художниками в будущем, но она открывает разные возможности для изучения, не в последнюю очередь того, существует ли конечное число апериодических моноплиток, ожидающих своего обнаружения.

«Нахождение такой моноплитки раздвигает границы сложности, которые, как известно, достижимы при мозаичном поведении одного замкнутого топологического диска», — пишут исследователи.