Что такое Байесовская сеть — примеры

Байесовская сеть (Bayesian network), также известная как вероятностная сеть или сеть Байеса, представляет собой графическую модель, которая используется для моделирования вероятностных отношений между набором переменных. Эта сеть основана на теореме Байеса о вероятности и теории вероятностей.

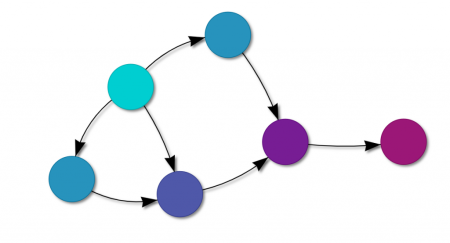
Основные компоненты Байесовской сети:

1. Узлы (вершины): Представляют переменные, которые моделируются, например, погодные условия, симптомы болезни и т. д.
2. Ребра (стрелки): Отображают статистические зависимости между переменными. Если переменная A напрямую влияет на переменную B, между ними проводится направленное ребро.
3. Таблицы условной вероятности (ТУВ): Каждая переменная в сети имеет таблицу условной вероятности, которая определяет вероятность значений переменной в зависимости от значений её родительских переменных.

Применения Байесовских сетей:

1. Диагностика и прогнозирование: Используется для диагностики болезней, прогнозирования погоды, финансовых анализов и т. д.
2. Принятие решений: Помогает принимать решения в условиях неопределённости, опираясь на вероятностные модели.
3. Рекомендательные системы: Используется для рекомендаций товаров, фильмов, музыки и т. д., учитывая предпочтения пользователя и их вероятности.
4. Анализ данных и управление знаниями: Для моделирования вероятностных отношений в данных и извлечения знаний из них.

Байесовские сети представляют собой мощный инструмент для моделирования и анализа вероятностных отношений в различных областях, где необходимо работать с неопределённостью и вероятностями.

Рассмотрим пример Байесовской сети, связанный с прогнозированием погоды.

Предположим, у нас есть следующие переменные:

1. Погода: Солнечно, Облачно, Дождь.
2. Температура: Высокая, Средняя, Низкая.
3. Влажность: Высокая, Нормальная.
4. Вероятность дождя: Высокая, Низкая.

Структура сети будет выглядеть следующим образом:

• Переменная «Погода» может зависеть от «Температуры» и «Влажности», так как эти факторы влияют на погодные условия.
• Вероятность дождя может зависеть от текущей погоды.

Таблицы условной вероятности определяют вероятности различных погодных условий в зависимости от температуры и влажности, а также вероятность дождя в зависимости от текущей погоды.

Например, если температура высокая, вероятность того, что погода будет солнечной, выше, чем вероятность того, что она будет облачной или дождливой. Если влажность высокая, то вероятность дождя возрастает.

Такая сеть может быть использована метеорологическими службами для прогнозирования погоды на основе текущих условий. Путем анализа зависимостей между различными факторами, модель может предсказывать, какие погодные условия наиболее вероятны в будущем, что помогает людям принимать решения, например, о том, как одеться или планировать активности на открытом воздухе.

Рассмотрим пример Байесовской сети с использованием формулы и условной вероятности.

Рассмотрим сеть для диагностики болезней.

Предположим, у нас есть две переменные:

1. Болезнь (Disease): Две возможные состояния, болен или не болен.
2. Симптом (Symptom): Две возможные состояния, присутствует или отсутствует.

Давайте представим, что у нас есть следующие вероятности:

• $P(D)$: Вероятность наличия болезни (предположим, 0.01, то есть 1% населения болеет этой болезнью).
• $P(S|D)$: Вероятность того, что симптом проявится, если человек болен (предположим, 0.9, то есть 90%).
• $P(S|\neg D)$: Вероятность того, что симптом проявится, если человек не болен (предположим, 0.2, то есть 20%).

Теперь, если мы хотим вычислить вероятность того, что человек болен, учитывая наличие симптома, мы можем воспользоваться формулой теоремы Байеса:

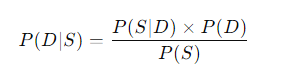
Здесь:

• $P(D|S)$ — это вероятность того, что человек болен, при условии наличия симптома.
• $P(S)$ — общая вероятность наличия симптома, которая может быть вычислена как $P(S|D)\times P(D)+P(S|\neg D)\times P(\neg D)$, где $P(\neg D)$ — вероятность того, что человек не болен.

Подставляя значения, мы можем вычислить вероятность того, что человек болен, при условии наличия симптома.

Это примерно показывает, как мы можем использовать Байесовские сети и теорему Байеса для оценки вероятностей различных событий при наличии определенных условий.