Математики, наконец, определили «кажущееся невозможным» девятое число Дедекинда

Математики, вооруженные суперкомпьютерами, наконец определили значение комплексного числа, которое ранее считалось невозможным для вычисления.

Число, известное как «девятое число Дедекинда» или D (9), на самом деле является 10-м в последовательности. Каждое число Дедекинда (Дедекиндово число) представляет собой количество возможных конфигураций определенного вида логической операции «истина-ложь» в различных пространственных измерениях. Первое число в последовательности — D(0), которое представляет нулевое измерение. Вот почему D(9), представляющее девять измерений, является 10-м числом в последовательности.

Числа Дедекинда экспоненциально увеличиваются для каждого нового измерения, что затрудняет их определение. Восьмое число Дедекинда, которое следует тем же правилам для восьми измерений, было вычислено в 1991 году.

Но из-за скачка вычислительной мощности, необходимой для вычисления девятого, некоторые математики сочли невозможным вычислить его точное значение.

Но теперь два несвязанных исследования разных научных групп — первое , отправленное на сервер препринтов arXiv 5 апреля, и второе , отправленное на тот же сервер 6 апреля, — сделали невозможное. Исследования — в каждом из которых использовался суперкомпьютер, но с разными программами — оба дали одно и то же число.

Результаты еще не были рецензированы. Но поскольку исследования пришли к одному и тому же выводу, есть «100% уверенность» в том, что число было правильно расшифровано, — заявил Леннарт Ван Хиртум, математик из Падерборнского университета в Германии и ведущий автор второй статьи.

Ван Хиртум и его коллеги защитили свою работу во время лекции в Падерборнском университете 27 июня.

Что такое числа Дедекинда?

Числа Дедекинда были впервые описаны немецким математиком Рихардом Дедекиндом в 19 веке. Цифры связаны с логическими проблемами, известными как «монотонные логические функции» (MBF).

Логические функции — это своего рода логика, которая может принимать в качестве входных данных только одно из двух значений — 0 (ложь) и 1 (истина) — и выдавать только эти два значения.

В MBF вы можете поменять местами 0 на 1 во входных данных, но только если это позволяет изменять выходные данные с 0 на 1, а не с 1 на 0. Числа Дедекинда — это выходные данные MBF, где входные данные конкретное пространственное измерение.

Эта концепция может быть довольно запутанной для нематематиков. Но можно визуализировать происходящее, используя формы для представления чисел Дедекинда для каждого измерения. Например, во втором измерении число Дедекинда относится к квадрату, тогда как третье может быть представлено кубом, четвертое и выше — гиперкубами.

Для каждого измерения вершины или точки определенной формы представляют возможные конфигурации MBF (см. рисунок ниже). Чтобы найти число Дедекинда, вы можете посчитать, сколько раз вы можете раскрасить каждую вершину каждой фигуры одним из двух цветов (в данном случае красным и белым), но с условием, что один цвет (в данном случае белый) не может быть помещен над другим (в данном случае красным).

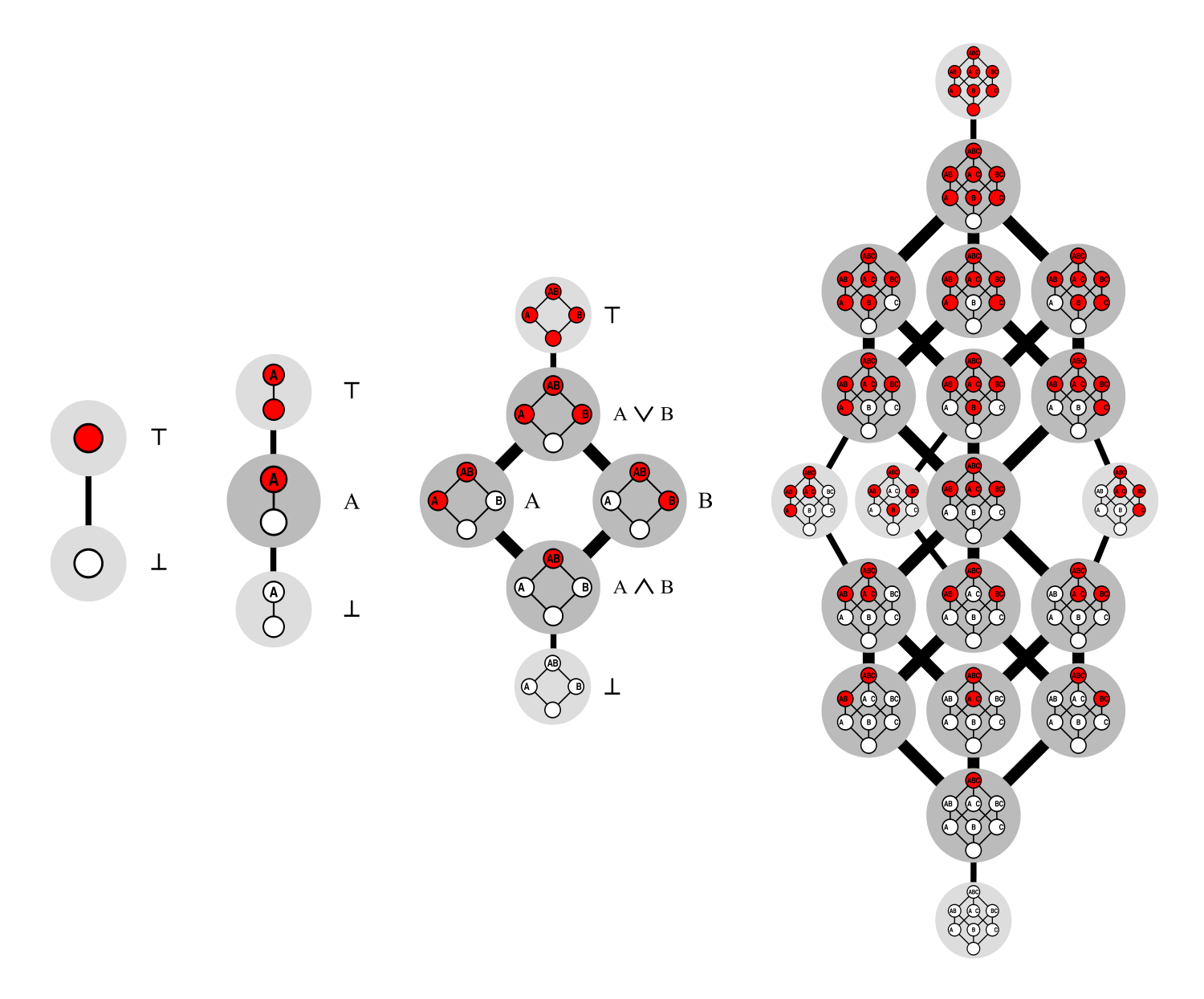
Для нулевых измерений фигура представляет собой всего лишь одну точку, а D(0)=2, поскольку точка может быть красной или белой. Для одного измерения фигура представляет собой линию с двумя точками и D(1)=3, потому что обе точки могут быть либо одного цвета, либо красного над белым.

Для двух измерений форма представляет собой квадрат, а D(2)=6, потому что теперь есть шесть возможных сценариев, в которых ни одна белая точка не находится над красной точкой. А для трех измерений форма представляет собой куб, а количество возможных конфигураций подскакивает до 20, поэтому D(3)=20.

Далее, по мере увеличения количества измерений гипотетическая форма становится все более сложным гиперкубом с экспоненциально большим числом результатов.

Значения следующих пяти чисел Дедекинда: 68, 7 581, 7 828 354, 2 414 682 040 998 и 56 130 437 228 687 557 907 788.

Новое идентифицированное значение для D(9) равно: 286 386 577 668 298 411 128 469 151 667 598 498 812 366.

Все более сложные расчеты

Леннарт Ван Хиртум и его коллеги работали над идентификацией D(9) более трех лет. Для этого они создали компьютерную программу нового типа, позволяющую суперкомпьютеру обрабатывать данные определенным образом. По их словам, если бы они использовал более простую программу, на выполнение расчетов могло уйти до 100 лет.

После создания своего компьютерного кода команда Ван Хиртума провела более четырех месяцев, используя суперкомпьютер в Левенском университете в Бельгии для обработки данных.

Однако расчеты на самом деле не заняли так много времени: характер программы означал, что она была склонна к ошибкам на полпути, а это означало, что команде приходилось постоянно перезапускать процесс.

Для сравнения, компьютер, использовавшийся в 1991 году для расчета D(8), был менее мощным, чем современный смартфон, и выполнил задачу примерно за 200 часов. По словам Ван Хиртума, современный ноутбук мог бы выполнить эти вычисления менее чем за 10 минут.

Ученые считают, что аналогичный скачок вычислительной мощности компьютера потребуется для вычисления 10-го числа Дедекинда. «Если бы мы делали это сейчас, это потребовало бы вычислительной мощности, равной общей выходной мощности солнца», — сказал Ван Хиртум, что делает расчеты «практически невозможными».

По его словам, требования к вычислительной мощности могут быть снижены за счет использования более сложных алгоритмов.

«Но мы как бы уперлись в стену из-за того, насколько сложными могут быть алгоритмы», — добавил он. Однако другие математики все еще надеются, что D(10) в конечном итоге можно будет рассчитать.