Королева чисел
«Девятка – хорошая загадка».
Русская пословица
Самыми загадочными свойствами в математике обладает число 9. Мимо него не смог пройти ни один исследователь чисел. Например, жрецы древнего Египта объясняли связь богов с земными делами с помощью чисел. Пифагорейцы считали число 9 пределом, внутри которого находятся все остальные числа. Не случайно в древней Греции было 9 богов и 9 муз. В культуре каждого народа имеется своё символическое обозначение этого числа. Верующие в знаке 9 находят духовное начало. Его трижды связывают со святой троицей. Девятку относят к мифическим числам, в которых скрыта духовная мудрость и ключ к пониманию мира.
Это число завершает однозначные числа и после него всегда начинается новый ряд. В числе Пи первые четыре цифры (3, 141…) в сумме дают число 9. В первой сотне его цифр 9 встречается 14 раз и по количеству занимает первое место наряду с другими числами.
К значению чисел в нумерологии я отношусь нейтрально. Это учение объясняет некую связь между числами и жизнью человека. И в них, якобы, заложено число судьбы. Эта гипотеза вызывает у меня определённый интерес. Но любые представления о роли и свойствах чисел требуют подтверждающих фактов и доказательств. Учёные относят нумерологию к мистике, так как не находят научных методов для её исследования. Я с уважением отношусь к творческим взглядам нумерологов. Поэтому любые гипотезы о свойствах чисел, в том числе самые невероятные, не считаю бесполезными. Все они имеют право на существование. В их теориях меня особенно интересует один вопрос. Могут ли цифры как-либо воздействовать на человека? На его судьбу числа влиять не могут, так как она зависит от других факторов. Но я не исключаю их духовного воздействия на людей. В числах реально находится информация, которая способна давать человеку различные сведения и вызывать у него своим содержанием определённые переживания и чувства. Других воздействий чисел на человека я не вижу.
Любые числа можно представлять двумя формами:
- В виде обозначения их цифровыми знаками, по количеству которых определяют их величины.
- В форме их составных частей. Их структура будет состоять только из двух видов цифр. Первой из них будет – 9, а вторая цифра будет выполнять роль остатка от первой.
Если исходить из этого представления, то все числа состоят из энного количества девяток и остаточных добавлений к ним. Например, число 54 состоит из 6 девяток. И больше в нём ничего нет. В числе 94 имеется десять девяток и к ним остаток – 4 единицы. Все другие знаки для подобных образований состава чисел не подходят.
Число 9 обладает в математике особыми свойствами, полными загадок. Его потенциал в математических действиях ещё долго не будет раскрыт в полном объёме. Я обратил внимание на это число в таблице умножения. В ней каждый столбец, озаглавленный множителями, не имеет общих правил решения. Все их нужно запоминать, кроме последнего столбца, озаглавленного цифрой 9. Только в этом перечне умножений действует универсальный метод для получения ответов. В нём умножение заменяется двумя вычитаниями. Результаты будут одинаковыми. Показываю его применение на конкретных примерах:
- 9 х 6 = 54. Решение: 6 – 1 = 5; 10 – 6 = 4.
- 9 х 7 = 63. Решение: 7 — 1 = 6; 10 – 7 = 3.
- 9 х 10 = 90. Решение: 10 – 1 = 9; 0 – 0 = 0.
Во всех примерах этого столбца нужно твёрдо усвоить два простых правила:
- Для получения первой цифры ответа нужно из второго множителя отнять единицу.
- Для получения второй цифры ответа нужно из 10 отнять второй множитель.
На схеме вся эта таблица представлена так:

Число 9 можно так же легко умножать и на любое двузначное число. Для этого нужно запомнить правила:
- Из двузначного числа нужно каждый раз отнимать число, которое на единицу больше первой цифры этого числа. Тогда получим ответ первых двух цифр.
- Третью цифру ответа узнаем, если вторую цифру двузначного числа отнять от 10.
Например, 9 х 84 = 756. Решение: 84 – 9 = 75; 10 – 4 = 6. Вместе получится 756.
9 х 47 = 424. Решение: 47 – 5 = 42; 10 – 7 = 3. Получится 423.
9 х 99 = 891. Решение: 99 – 10 = 89; 10 – 9 = 1. Получится 891. Все остальные примеры решаются таким же способом. Я поместил их в одной таблице. Она проста в усвоении и смотрится так:
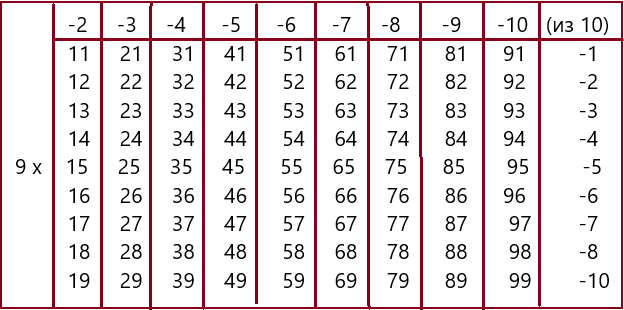
Во всех ответах сумма трёх чисел будет равна 9. (9 х 38 = 342. 3 + 4 + 2 = 9). Сумма цифр в ответе будет всегда равна девяти, если 9 умножать на любое другое число. (9 х 4567 = 41103; 4 + 1 + 1 + 3 = 9). Каждый пример из этой таблицы можно научиться превращать в трёхзначное число всего за 2-3 секунды.
Например, из цифры 13 (чёртовой дюжины) получится число 117. Я пытался его расшифровать, но в нём не оказалось слов. Был лишь намёк на смысловое понятие, обозначающее разумный сигнал. Если на последние две цифры трёхзначного числа 117 продолжать воздействовать числом 9, то получится следующий ряд:
9 9 9 9 9 9 9 9 9 9 9
117 153 477 693 837 333 297 873 657 513 117
Число 117 вновь повторится через 9 трёхзначных чисел. Сумма знаков каждого числа будет равна 9. Любое двузначное число можно превратить в трёхзначное без участия числа 9. Результат будет одинаковый. Для этого нужно использовать два вида вычитаний. Например, 39 – 4 = 35; 10 – 9 = 1. В результате этих действий 39 превратится в число 351. Эти простые действия меняют статус числа. Чтобы проверить его правильность нужно 9 х 39 = 351.
В этом случае участие девятки в создании трёхзначного числа можно считать условным. При этих преобразованиях число 9 будет играть роль «математического катализатора». Оно только подсказывает во что превратится преобразование различных чисел и «отходит в сторону», предлагая другим знакам продолжать вычисления. У этого «катализатора» роль «вещества» выполняет число 9. Проявление этого свойства значительно упрощает процесс умножения чисел.
Если существует способ превращения двузначного числа в трёхзначное, значит может быть обратное его преобразование.
Для примера возьмём число 57 и превратим его в трёхзначное число.
57 – 6 = 51; 10 – 7 = 3. В результате получим число 513. Теперь в обратном порядке это число превратим в двузначное.
51 + 6 = 57; 10 – 3 = 7. Итог – число 57.
Такого же превращения можно добиться и с участием числа 9, если не него разделить 513 (513: 9 = 57). Возникает вопрос о практическом применении этих превращений, которым «покровительствует» девятка. Их эффективность можно доказать только конкретными примерами:
153 х 477 = 72981. Числа 153 и 477 преобразуем в числа 17 и 53.
Решение:
17 х 53 = 901; 81 х 901 = 72 981. Или 80 х 901 = 72080 + 901 = 72981.
В этом примере в преобразовании двух чисел могли участвовать две девятки, которые вместе составили число 81. Краткость и простота этого вычисления не вызывает сомнений. Этот факт доказывает преимущество данного алгоритма действий.
Базовое число в математике
Нумерология относит к базовым числам однозначные числа от 0 до 9. Наука в практике вычислений понятие базового числа не применяет. В математике существуют только базовые элементы, которые начинаются с единицы при подсчёте предметов. Их называют натуральными числами от 1 до бесконечности.
Пусть не обижаются на меня математики, но я отношу к базовым трёхзначные числа, образованные с помощью указанных выше действий. Только с помощью их можно поменять порядок вычислений и отказаться от традиционного «столбика». Эти базовые числа обладают ключевыми свойствами при математических вычислениях. Они значительно упрощают сам процесс математических действий со всеми числами, которые имеют «родственные» связи с девяткой.
Самым сложным из четырёх арифметических действий является умножение чисел. С его помощью можно заменить сложение одинаковых чисел. Гораздо легче применять в математике сложение, вычитание и деление.
Простейшим алгоритмом в получении результатов считают «умножение в столбик». Другое название — перекрёстный метод умножения. Этот стандартный приём в математике применяют все ученики начальных школ. Я тоже прошёл через эти однообразные математические испытания. При этих действиях всегда применяют таблицу умножения. Этот процесс не даёт разгуляться творческим порывам и не создаёт нагрузку для ума в получении результатов. Самое главное здесь – не допустить механической ошибки.
Например, при умножении четырёхзначных чисел к таблице обращаются 16 раз. Алгоритм умножения можно значительно упростить с помощью базовых трёхзначных чисел.
Возьмём самые простые примеры:
- 18 х 48 = 864.
Решение: 9 х 48 = 432 (или: 48 – 5; 10 – 2). В числе 18 имеется две девятки, а 48 превращается в базовое число 432.
2 х 432 = 864.
- 81 х 93 = 7533.
В числе 81 имеется 9 девяток, а 93 превратим в число 837. 9 х 837 = 7533.
- 48 х 37 = 1776. В числе 5 девяток и 3 в остатке. 37 превращаем в 333.
Решение:
5 х 333 = 1665 + 111 = 1776.
3 х 37 = 111.
- 270 х 368 = 99360. В числе 270 – 30 девяток.
Решение: 9 х 368 = 3312; 30 х 3312 = 99360.
- 999 х 67 = 66 933.
Базовое число в это примере 603, а в числе 999 — 111 девяток. Решение:
600 х 111 = 66600 + 333 = 66933.
3 х 111 = 333;
- 9999 х 89 = 889911.
Решение: 801(базовое число).
1111 х 800 = 888800 + 1111 = 889911.
- 104 х 427 = 44408. (В числе 104 – 11 девяток и 5 в остатке).
Решение: 9 х 427 = 3843 х 11 = 42273 + 2135 = 44408.
5 х 427 = 2135;
- 92 х 72 = 6624. (В числе 92 – 10 девяток).
Решение: 10 х 648 + (2 х 72) = 6624.
- 576 х 832 = 479232. (57 + 7 = 64; 83 + 10 = 93).
Решение: 832 заменяем на 837 (832 + 5).
64 х 93 = 5952 х 81 = 482112 – 2880 = 479232.
5 х 576 = 2880.
- 360 х 5448 = 1961280. (В числе 360 — 40 девяток)
Решение: 9 х 5448 = 49032 х 40 = 1961280.
Если оба множителя состоят только из девяток, тогда один из них нужно превратить в базовое число и на него умножить количество девяток другого числа.
Пример: 54 х 36 = 1944. Решение: 6 х 324 = 194.
Если один множитель состоит из девяток, а другой – из девяток и остаточного числа, то можно применить метод:
Например: 36 х 74 = 2664. Решение: 4 х 666 = 2664. В числе 36 было 4 девятки, а из числа 74 образовалось базовое число 666 (число зверя). На это число умножил 4 и получил ответ.
У меня возник интерес к алгоритму умножения двух чисел зверя.
666 х 666 = 443556. Оба «звериных» числа разделил на 9 и получил дважды 74.
Решение: 74 х 74 = 5476; Или 74 в квадрате равно 5476.
5476 х 81 = 443556. Или 80 х 5476 + 5476 = 443556.
Возьмём пример, когда множители состоят из большого количества девяток.
468 х 567 = 265356. Оба множителя разделил на 9 и получил числа 52 и 63.
Решение: 52 х 63 = 3276; 3276 х 81 = 265356. Или: 80 х 3276 + 3276 = 265356.
Я отношу обнаруженное при вычислениях число 74 к «маске» числа 666. Если его разделить на 6, то получим ответ: 12, 333333… В нём оказалось две шестёрки, а третью шестёрку будут создавать бесконечные пары троек.
Мне стало интересно. Что на самом деле, кроме зверя, обозначает число 74?
Мои поиски остановились на следующих фактах:
- Это число является официальным кодом Челябинской области РФ.
- Известно «Письмо семидесяти четырёх», как название двух документов: «Письма писателей России к Верховному Совету СССР, Верховному Совету РСФСР, делегатам ХХVIII Съезда КПСС, подписанные литераторами после избрания М.С. Горбачёва президентом СССР.
- В математике число является двузначным, а также недостаточным и полупростым числом.
- В таро число соответствует карте Теней Аркан 74 «Серп Сатурна». Эта карта символизирует чёрную полосу, появление трудностей и тяжкие лишения.
- В философии оно символизирует тьму и отсутствие света. А на иврите означает слова «ночь» и «царь».
- При обозначении букв цифрами выдаёт имя «Люцифер».
- В нумерологии число 74 принимает роль мученика.
- В Библии упоминается дважды. Но 74 раза в ней встречается слово «демон» и глагол «страдать».
- В 1974 году из страны был выслан писатель А.И. Солженицын за книгу «Архипелаг ГУЛАГ», в которой было показано жестокое содержание заключённых в тюрьмах и лагерях на территории СССР.
Из этих фактов видно, что в данном числе кроется больше зла, чем добра. Если бы все знали о реальном значении скрытого под этой маской лица. В «Апокалипсисе» (гл. 13: 18) Иоанн Богослов выразил своё предчувствие о негативной роли числа 666, называя его «числом зверя». Он предлагал сосчитать это число, чтобы понять его внутреннюю негативную сущность.
Все представленные примеры в этой статье могут решаться устно. Подобные методы вычислений на приведённых примерах не заканчиваются. Их нужно продолжать исследовать, чтобы находить в числах другие неизвестные свойства. В них всегда будет главенствовать королева всех чисел 9 (девятка). И все, кто увлекается устным счётом, могут взять эти методы вычислений на заметку.
Редакция не несёт ответственности за содержание предоставленного материала. Мнение авторов публикаций в разделе «Авторский материал» не обязательно отражает точку зрения редакции.
