Кубок Пушкина
«Эти числа мерами сочти. Их линии умеют разделять
жрецы. Им маяки давали луч, как черта — аллею.
Шли у пар следы за призраками грёз. И у края среза
уже маячили узорами фигуры Божьи смысла и начала.
А их цепи линий брали из шкалы цифири…»
(Из отрезка числа Пи – 2 млн. 622-я тысяча цифр после
запятой. Его расшифровка выполнена автором статьи)
О «свободе» чисел
Любые числа имеют внутренние невидимые свойства и способны самостоятельно выражать свою логику и смысл. Навязывание цифрам каких-либо правил и образов превращает их в «рабов» фантазий человека. Например, существует немало методик визуализации числа Пи с помощью цветных абстрактных картин. К каждой цифре прикрепляется один из 10 цветов. А их беспорядочное сочетание создаёт цветовое многообразие.
Эти картины очень красивы, но они «мертвы». В них никогда не будет признаков разума или логики смысла. Если числам навязать какие-либо надуманные образы, получится тоже самое. В результате возникнут фантастические картинки, автором которых будет только человек.
Я не являюсь сторонником подобных методик. Мои исследования направлены на поиск ещё не раскрытых свойств чисел, в глубинах которых может находиться разумное начало. Функции чисел гораздо шире их математического применения. Например, в математике они подчиняются известным законам и правилам. А «свободные» знаки в константе начинаются после запятой.
Первые её 39 цифр могут определять точность вычислений. Знаки, следующие за ними, полностью покидают этот материальный мир и переходят в сферу абсолютной свободы духа. При этом все они будут умещаться в единице измерения, как символе вселенной. В своих предыдущих статьях я приводил примеры расшифровки чисел и нахождения в них сведений об окружающем мире.
Меня заинтересовал конкретный вопрос: может ли число выдавать разумные идеи языком графики? Я исходил из того, что каждой цифре соответствует реальная мера длины, выраженная в любых единицах измерения. Если перевести десятичную систему счисления (0 1 2 3 4 5 6 7 8 9 10) на длину цифровых отрезков, то получится следующий набор линий:
(0 . 1__ 2 ____3______ 4________ 5__________ 6____________ 7 ______________8________________ 9__________________ 10____________________).
Отдельная цифра 0 обозначена точкой, а все остальные – отрезками. Графика линий широко применяется архитекторами, художниками и конструкторами. С их помощью можно создавать форму и пространство. Если сложить столбиком параллельные линии различной длины, то на границах их окончаний образуется контур фигуры. Количество графических изображений будет безгранично, как и разнообразие чисел.
В ходе отработки этой методики я убедился, что линии могут быть носителями разумной информации. А язык графики чисел образует своё визуальное информационное поле. Я подбирал расстояние между параллельными линиями методом проб и ошибок. В результате оптимальной пропорцией оказалось число «золотого сечения» к единицам измерения (1:1,6). Например, при длине линий в сантиметрах, расстояние между ними будет 1,6 cм.
Если натуральный ряд чисел от 0 до 9 расположить симметрично по отношению к центральной вертикальной оси, то получится контур треугольника. Для его усиления нужно соединить концы линий правой и левой стороны.
В этой методике я использовал принцип симметрии. Все линии при построении делятся на две равные части по обе стороны от центральной оси. Примером является эта схема. Рисунок № 1.
Симметрия является наиболее распространённой формой образования объектов материального мира. Например, у всех видов животных и насекомых правая и левая часть (в длину) одинаковы. Этому принципу «подчиняется» горбатый верблюд и сороконожка. То же самое наблюдается и у растений. Она гораздо привычнее восприятию человека, так как создаёт красоту и гармонию.
Симметрия в обществе проявляется в равновесии политических сил. К нему стремится любое государство и в целом человечество. Диктат одной главной силы в мире является исключением из правил и не может быть постоянным. Против этого центра силы неизбежно возникнут противовесы. Равновесие частей любого объекта является законом мироустройства.
Кубок Пушкина
Этот принцип симметрии я стал применять при переводе чисел на графический язык. В качестве примера выбрал две даты, известные всему миру. Это цифры рождения (6 июня 1799 г.) и гибели А.С. Пушкина (10 февраля 1837 г.). Я решил узнать, что «говорят» эти два числа (6 6 1 7 9 9 и 10 2 1 8 3 7) о гении русской литературы на графическом языке. И могут ли они как-либо «откликаться» на сущность событий?
Боковые границы линий цифр первого числа, к моему удивлению, отчётливо показали контур кубка. Так он выглядит на рисунке № 2.
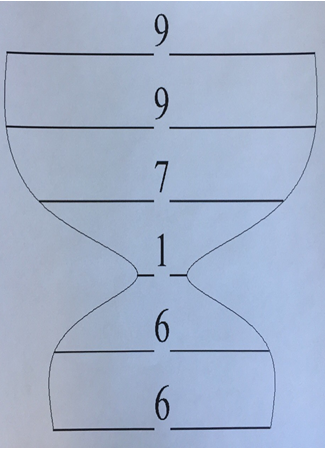Кубок является символом духовности и бессмертия, а также особой почести человеку за его заслуги. В средние века их вручали рыцарям за победы на турнирах. У Пушкина было особое почтение к этому символу. Он неоднократно обращался к нему в своих произведениях.
В стихотворении «Заздравный кубок» поэт предлагает поднять его за «Здравие славы», что на деле означает благодарение Богу за своё рождение и молодость. Например, дата рождения А.С. Пушкина встречается в первых 4-х млн. цифр числа Пи 12 раз после запятой.
Получается, что цифры «выразили» сам факт его рождения символом высшего отличия и почитания. И с первого дня предугадали» в нём будущую славу гениального мастера слова, непобеждённого никем по настоящее время. Перевод даты гибели А. Пушкина после дуэли с цифрового языка на язык графики показал контур светильника. Он выглядит так: рисунок № 3.
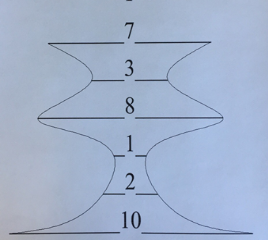
Данный предмет упоминается в Библии 54 раза. В ней говорится: «…радость
наша исчезла, свет светильника нашего угас…» ЗЕзд 10:22.
Светильник является знаком светлого человека, границей его жизни и смерти. Гибель А. Пушкина воспринимается, как угасший свет гения поэзии. И эта горькая утрата никогда не будет восполнена.
«Угас, как светоч, дивный гений,
увял торжественный венок.»
Написал М. Лермонтов в стихотворении «Смерть поэта».
Являются ли эти графические фигуры по отношению к поэту случайным совпадением? Эту загадку я объяснить не в состоянии.