Новое уравнение для более точного отслеживания небесных объектов

Исаак Ньютон был первым, кто предположил, что гравитация может искривлять свет, но Альберт Эйнштейн развил эту идею в своей общей теории относительности 1915 года, которая точно предсказала угол, под которым будет отклоняться свет звезд при прохождении вблизи Солнца.
Недавно профессор Оскар дель Барко Новилло из Университета Мурсии в Испании и его коллеги разработали точное уравнение для расчета угла гравитационного искривления света, учитывающее положение как источника света, так и наблюдателя на любом расстоянии от статической гравитационной массы.
Такое развитие имеет важное значение, поскольку оно может помочь астрономам точно определить местоположение астероидов и других мелких объектов в Солнечной системе. Это приведет к более точным расчетам их орбит вокруг Солнца, что облегчит идентификацию объектов, которые могут потенциально угрожать Земле.
Эти объекты включают в себя те, что находятся в поясе Койпера, регионе за орбитой Нептуна, заполненном ледяными телами, такими как Плутон и другие карликовые планеты.
Кроме того, есть Облако Оорта, огромная сферическая оболочка ледяных объектов, которая находится на самом внешнем краю Солнечной системы и является домом для многих долгопериодических комет.
На основе модели геометрической оптики исследование представляет точное уравнение для расчета угла гравитационного искривления света (GBL), вызванного массивным статическим объектом, таким как Солнце или планеты в Солнечной системе. Этот прорыв может иметь более широкие последствия, повышая точность определения местоположения далеких звезд и уточняя орбиты малых объектов солнечной системы, таких как астероиды.
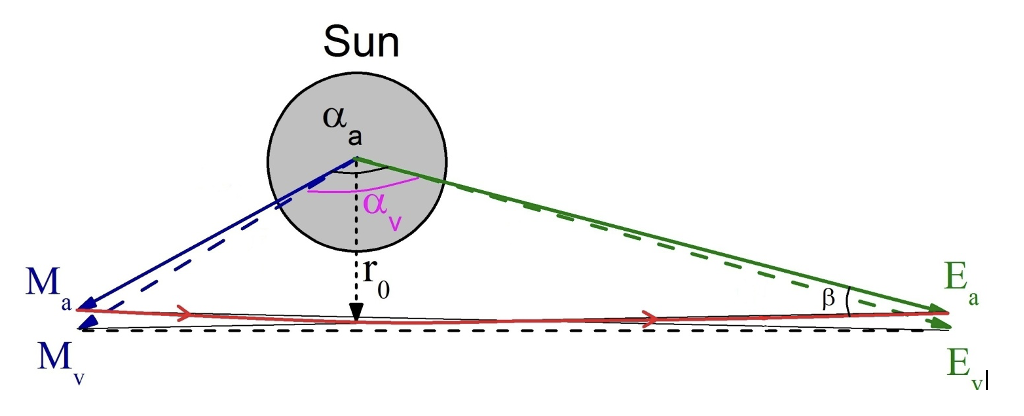
Профессор Оскар Новилло сказал: «В результате этого могут выиграть различные разделы астрономии и астрофизики, такие как небесная механика или звездная динамика».
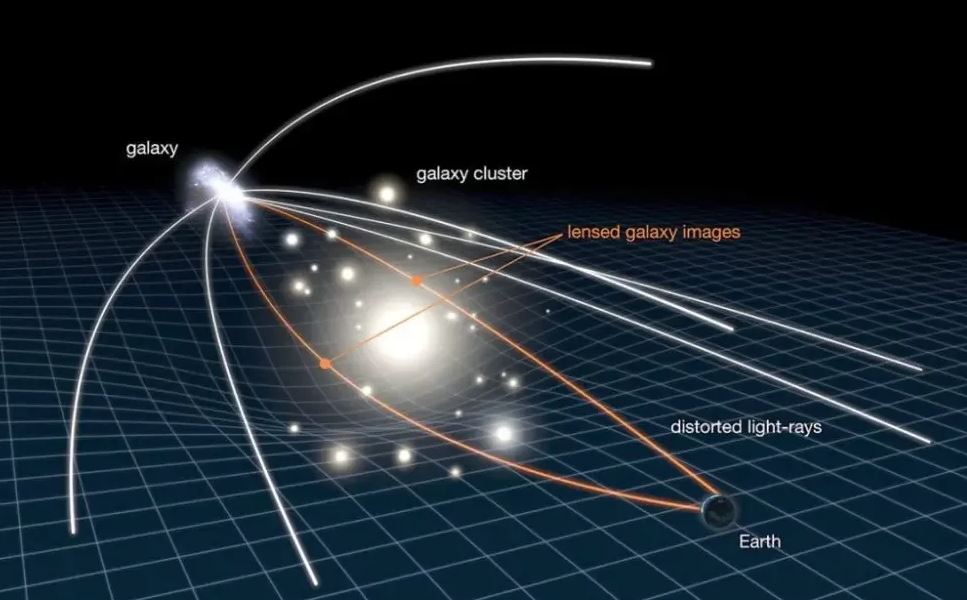
Новый расчет также может позволить более точные измерения местоположения далеких галактик, искаженных и увеличенных промежуточной массой, такой как скопления галактик, посредством слабого гравитационного линзирования. Это достижение особенно важно для астрометрии, раздела астрономии, сосредоточенного на точном измерении небесных положений и движений.
Кроме того, это может привести к созданию более подробных карт распределения масс внутри скоплений галактик, особенно с учетом работы миссии «Евклид» Европейского космического агентства.
«Основное значение нашего нового уравнения заключается в его высокой точности расчета угла GBL из-за статической гравитационной массы по сравнению с предыдущими приближенными уравнениями, основанными на постньютоновском формализме», — говорит Оскар Новилло. «В результате это может сыграть важную роль в определении точного местоположения малых небесных объектов в нашей Солнечной системе и, следовательно, в более точном определении их орбит вокруг Солнца».
Таким образом, новое исследование должно быть важным для астрономов и астрофизиков, работающих над сверхточными астрометрическими измерениями, особенно в исследованиях гравитационного линзирования.
Есть надежда, что уравнение даже может дать более точное местоположение ближайшей к нашей планете звезды после Солнца, называемой Проксима Центавра, которая находится на расстоянии 4,25 световых лет от нас и, как полагают, имеет три экзопланеты, вращающиеся вокруг нее. Если ее точное местонахождение будет определено, это также поможет точно оценить орбиты ее планет.