Поединки с числами
«Математику уже затем учить надо,
Что она ум в порядок приводит».
М.В. Ломоносов
Число является основным абстрактным понятием математики. Роль чисел постоянно расширяется, и никто не знает предела их применения. В практике любых количественных вычислений существует множество приёмов, которые помогают в их решении. В достижении результатов многое зависит от исходных данных. Они определяют сложность решения заданий.
В последнее время много внимания уделяется ментальной математике. Быстрый счёт в уме приучает мозг к дисциплине и логике мышления. Он развивает интеллект, память и творческие рамки возможностей человека. Особенно это полезно для учащихся школ и всем, кто увлекается вычислениями в уме на скорость.
К сожалению, устный счёт в наших школах практически не применяется. Примеры на умножение чисел решаются учениками, как правило, «столбиком» и в письменном виде.
На уроках математики учащихся с детских лет заставляют заниматься рутинной и механической работой по установленным правилам. Им не нужно сильно напрягать свои мозги, чтобы решать на бумаге подобные примеры. Гораздо больше пользы для развития гибкости мышления и концентрации внимания детей будет при решении двух примеров в уме, чем 20 — в тетради.
Возможно, по этой причине у многих учащихся теряется интерес к математике. А этот предмет относится к самой перспективной и таинственной науке в мире. Числа и слова в своей гармонии являются духовными корнями человечества.
В своей практике увлечения математикой я использовал свои приёмы в решении математических примеров. Самыми трудными из них считаю задания на умножение и возведение в степень. Мною был установлен рекорд России по ментальной математике: «Возведение в степень (2-9) наибольшего количества двузначных чисел за пять минут. Результат — 8 чисел. Место фиксации рекорда: шоу «Я могу». Первый канал. г. Москва 06.11.2017 год.
В этой статье показываю только те примеры, которые реально решаются в уме. Каждый из них можно выбирать по своему усмотрению.
Умножение двузначных чисел
Вариант 1
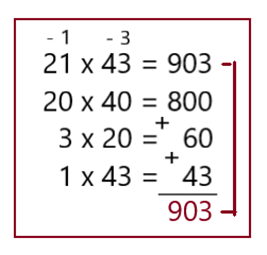
В этом примере множители превращены в десятки, которые легко перемножить. Затем выполняются два действия с цифрами 1и 3. Они решаются в двух вариантах: 1) (3х20) + (1х43) = 103. 2) (3х21) + (1х 40) = 103. Для получения ответа к числу 800 прибавляется 103.
Вариант 2
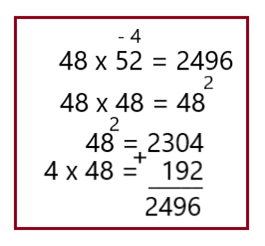
В этом варианте, после изъятия цифры 4 у второго множителя, получаются два одинаковых числа – 48.
Их можно возвести в квадрат. Затем к полученному результату добавляем число 192 и получаем общий ответ.
Вариант 3
Здесь второй множитель уменьшается до числа 11. Любое двузначное число, умноженное на 11, легко решается по схеме: 6 + 8 =14. Эта сумма ставится между
цифрами 6 и 8 и получится – 748.
Вариант 4
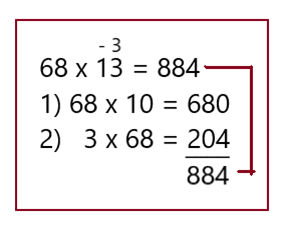
Второй множитель числа превращается в число 10 и перемножается с первым множителем. К результату прибавляем недостающее число 204 и получаем ответ.
Вариант 5
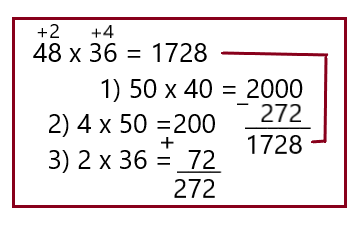
Данный пример решается аналогично первому варианту.
Возведение в квадрат двузначных чисел
Вариант 1
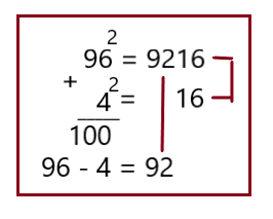
В числе 96 до ста не хватает 4 единицы. 4 в квадрате даёт половину ответа (16).
Если от 96 отнять 4, то получим первую часть ответа.
Вариант 2
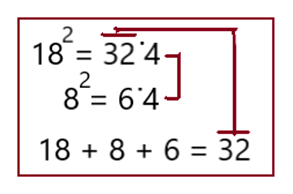
Все числа от 11 до 20 решаются по этой схеме. Все цифры больше 10 возводятся в квадрат.
Последняя цифра 4 совпадает с концовкой ответа. А его первые две цифры (32) получены от сложения указанных ниже чисел.
Вариант 3
Десятки легче умножать на двузначное число. Поэтому число 67 можно увеличить до 70. А затем из полученного результата отнять число 201 для получения ответа.
Деление чисел
Вариант 1
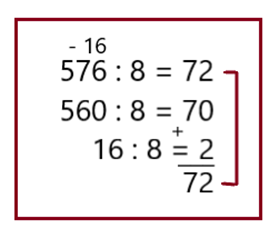
Кроме традиционных методов деления чисел столбиком можно использовать приёмы, показанные в вариантах: 1,2,3. При устном счёте сокращается время на их решение.
Вариант 2
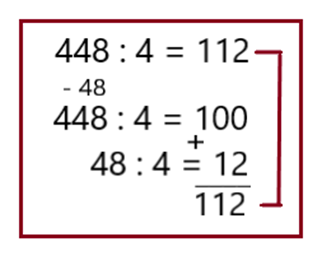
Вариант 3
Словесно-цифровая математика
Вариант 1
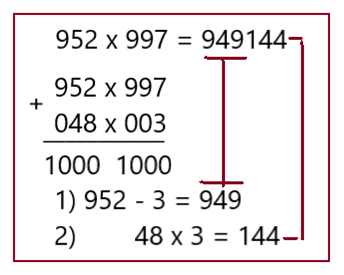
В приведённых ниже вариантах показаны примеры умножения больших чисел. Все они требуют значительной концентрации внимания, чтобы удерживать в памяти ряды цифр и порядок их действий. Показанные ниже приёмы позволяют облегчить их решение.
Примером является вариант 1. Во всех остальных случаях можно использовать словесно-цифровой метод. Он состоит в кодировании рядов чисел в тексты. Разработано достаточно много их способов. Самым распространённым является буквенно-цифровой способ, когда каждой цифре присваивается первая буква их названий (7 – С). Из букв этих цифр составляются слова. Их гораздо легче запоминать, чем числа.
Этот метод закрепляется тренировками. Начинать нужно с умножения однозначного числа на многозначное. За результатом любого вычисления должны тянуться отдельные слова, как хвост за кометой. Каждое слово будет заменять 2-3 цифры. Их проще запомнить. Ниже показаны все варианты, где этот метод можно применить.
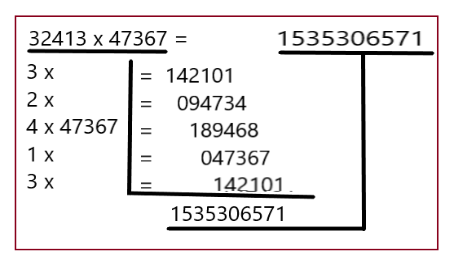
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Возведение в квадрат трёхзначных чисел
(приёмы возведения)
Вариант 1
Вариант 2
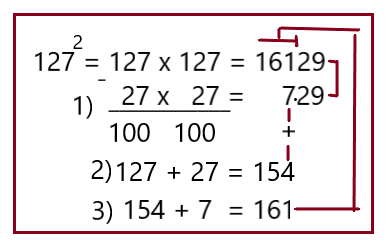
Вариант 3
Вариант 4
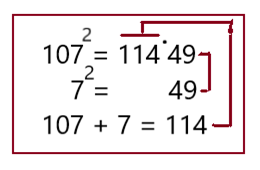
Все 3-значные числа от 100 до 200 решаются простым способом, показанном на схемах вариантов: 5,6,7,8.
Вариант 5
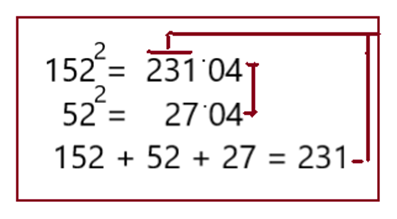
Вариант 6
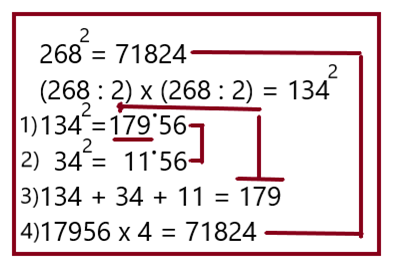
Вариант 7
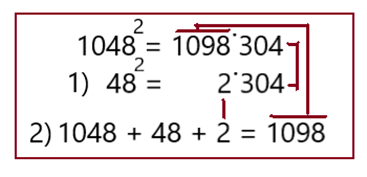
Вариант 8
В этом варианте решение состоит из двух частей. Вначале из 10000 выделяется число 132 и возводится в квадрат. В результате получим пять цифр, 4 из которых относятся к концовке общего ответа. Во второй части решения из 100 выделяем число 32 и возводим его в квадрат и далее решаем по такой же схеме.
Таблица квадратов чисел
В математике широко применяется таблица умножения, которую учат все. Не менее важна и таблица квадратов двузначных чисел. Если убрать из неё десятки, то количество примеров сократится до 81. Её всю можно закодировать в слова. Тогда каждый пример будет состоять из 2-3 слов. Одно слово будет принадлежать числу, которое будет возводиться в степень, а 1-2 – ответу. Последнюю цифру ответа включать не нужно. На запоминание этой словесно-цифровой таблицы потребуется немного времени. Я выучил её за 3 часа.
Она позволяет решать квадраты этих чисел мгновенно и выдавать ответ за 2-3 секунды. Эту таблицу может составить любой желающий, по схеме, которую предлагаю ниже. Из своей таблицы выбрал 7 примеров, которые показались мне более интересные.
Знание таблицы квадратов позволяет быстро решать в уме приведённые ниже примеры (варианты 1,2,3).
Вариант 1
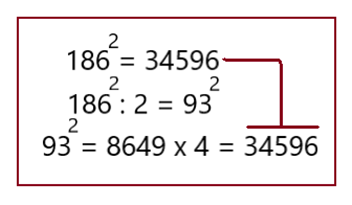
Вариант 2
Вариант 3
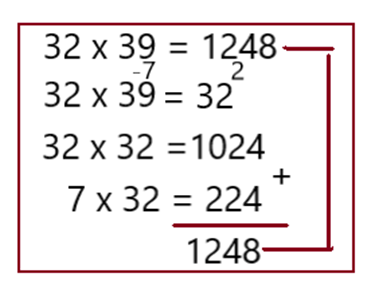
Универсальный алгоритм решений
При умножении многозначных чисел в уме многие примеры даже математики считают не подъёмными. Например, немногие могут умножить в уме числа из 7-10 знаков. В настоящее время мировой рекорд по умножению 10-значных чисел в уме принадлежит России. Пример был решён за 14 минут 31 секунду.
Человек давно научился обращаться с неподъёмными грузами. Он использует для этого два способа: 1. Применяет рычаг. 2. Делит груз на части и переносит его. В математике вместо рычага к большим числам обычно применяют письменный метод.
Умножение чисел, как правило, считается единым процессом и на отдельные самостоятельные части не дробится. Например, если всю операцию при умножении 5-значных чисел разделить на 10 отдельных частей, то их решение облегчится в 10 раз! На каждую цифру ответа будет проводиться отдельное вычисление. Такой метод позволит любому человеку решать подобные примеры в уме без особых усилий. Для этого требуется разработка универсального алгоритма действий для каждого знака ответа. Количество алгоритмов решений будет равно количеству знаков в ответе.
При освоении этой методики не будет считаться фантастикой умножение в уме 15-значных чисел. В ответе будет 30 знаков, которые потребуют 30 отдельных цифровых решений. Алгоритмы на каждое решение можно реально запомнить и применять их каждый раз в уме. По такой же методике можно разработать алгоритм возведения двузначного числа в 10-ю и более высокую степень. И такие возможности в практике имеются.
Разработать и усвоить универсальные алгоритмы решений любых чисел можно по образцу умножения двузначных чисел. Например, 38 х 64 = 2432. На схеме результаты умножения каждой пары цифр помечены знаками: десятки – 0, а единицы – 1. В центре образовались два столбика из трёх цифр, которые складываются.
Например, чтобы получить третью цифру ответа нужно перемножить 3 пары цифр: 3х4(1), 8х4(0) и 8х6(1). В скобках указаны значения единиц и десятков, которые складываются. 2(1) + 3(0) + 8(1) =3. Такие же действия проводятся для вычисления 2-й цифры ответа. Если оба множителя обозначить номерами (1234), то получится алгоритм решения при умножении любых двузначных чисел (см. правую сторону схемы).
Вариант 1
Вариант 2
Во втором варианте показан алгоритм решения, когда множители обозначаются буквами (ab).
Вариант 3
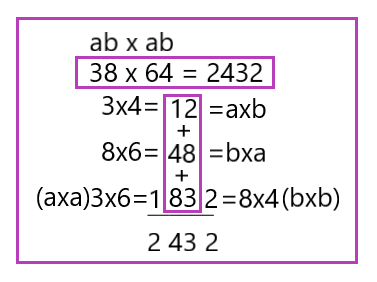
В этом варианте для получения результата достаточно сложить в уме три двузначных числа: 12+48+83=143. При решении подобных примеров эти три числа будут меняться. Например, нужно перемножить 46 х 78 = 3588. Для решения складываются числа: 32 + 42 + 83 = 158. Этот порядок умножения цифр необходимо запомнить с помощью тренировок. При устном решении этих примеров требуется не более 20 секунд.
Таким же способом можно разработать и запомнить алгоритмы решений при умножении других чисел.
Автор Владимир Кондряков.