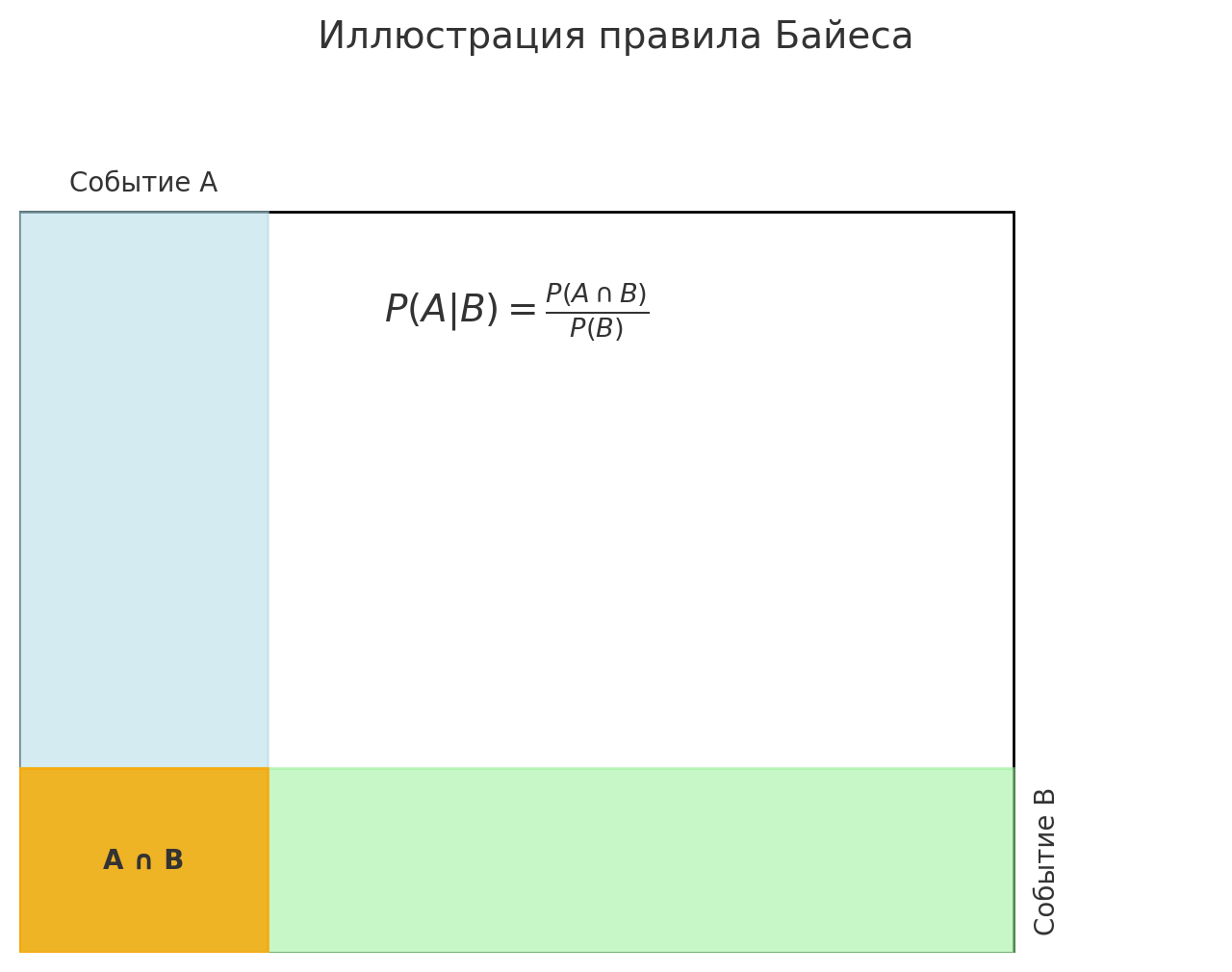
Правило Байеса — как его понять?

Правило Байеса — это фундаментальное правило теории вероятностей, которое позволяет пересчитывать вероятность события с учётом новой информации. Оно связывает априорные вероятности (то, что мы знали до получения данных) с апостериорными вероятностями (то, что мы думаем после получения данных).

Формула правила Байеса выглядит так:

$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$$

Где:

P(A∣B)P(A|B) — апостериорная вероятность: вероятность события A, если произошло событие B;

$P(B|A)$

— вероятность наблюдать событие B, если истинно событие A (правдоподобие);

P(A) — априорная вероятность события A (до получения информации о B);

P(B) — общая вероятность события B (нормирующий множитель).

Пример

Предположим, есть редкая болезнь, которой болеет 1 человек из 1000 (P(A)=0.001).

Существует тест, который показывает положительный результат в 99% случаев, если человек болен (P(B|A)=0.99), и ошибается в 2% случаев, если человек здоров (P(B|\neg A)=0.02).

Если тест показал «положительно» (B), какова вероятность, что человек действительно болен?

$$P(A|B) = \frac{P(B|A)\cdot P(A)}{P(B|A)\cdot P(A) + P(B|\neg A)\cdot P(\neg A)}$$

Подставляем:

$$P(A|B) = \frac{0.99 \cdot 0.001}{0.99\cdot 0.001 + 0.02\cdot 0.999} \approx 0.047$$

То есть даже при положительном тесте вероятность болезни всего около 4,7% — из-за ее редкости.

Таким образом, правило Байеса помогает корректно интерпретировать вероятности, учитывая новые данные. Его широко применяют в медицине (диагностика), статистике, машинном обучении, судебной экспертизе и даже в повседневной жизни.

Ниже более простые примеры, без формул.

Представьте, что вы видите на улице человека с зонтами в руках.

• Априорное знание: вы знаете, что в вашем городе обычно дождь идёт редко — всего несколько дней в месяце.
• Новая информация: но сейчас вы заметили, что человек несёт зонт.
• Апостериорный вывод: вероятность того, что на улице идёт дождь, сразу выросла, потому что наличие зонта — это дополнительный признак, который вы учитываете.

То есть правило Байеса работает так: сначала у вас есть общее представление о ситуации (дождь редкий), потом появляется новое наблюдение (зонт), и вы пересматриваете свою уверенность (дождь сейчас более вероятен).

Теперь возьмем пример из медицины:

Пациент приходит к врачу с жалобой на кашель.

• Априорное знание: врач знает, что в этом сезоне большинство случаев кашля связано с простудой, а не с пневмонией.
• Новая информация: у пациента высокая температура и хрип в лёгких.
• Апостериорный вывод: вероятность пневмонии возрастает, потому что новые признаки сильнее указывают на неё, чем на обычную простуду.

А теперь пример из расследований:

В городе произошло ограбление, и очевидцы сообщили, что преступник был в красной куртке.

• Априорное знание: в городе тысячи людей, и только у некоторых красные куртки.
• Новая информация: полиция останавливает человека в красной куртке неподалёку от места преступления.
• Апостериорный вывод: вероятность, что именно этот человек причастен к ограблению, повышается, но всё равно остаётся далеко не 100%, ведь красные куртки носят и невиновные люди.