Ученые создали самый сложный лабиринт в мире

Взяв принципы фрактальной геометрии и стратегической игры в шахматы, ученые-физики создали, по их словам, самый невероятно сложный лабиринт из когда-либо созданных.

Научная группа под руководством Феликса Фликера из Бристольского университета создала маршруты, называемые гамильтоновыми циклами, в шаблонах, известных как мозаика Аммана-Бинкера. В итоге получились сложные фрактальные лабиринты, которые, по словам исследователей, описывают экзотическую форму материи, известную как квазикристаллы. И все это было вдохновлено движением коня по шахматной доске.

«Когда мы посмотрели на формы построенных нами линий, мы заметили, что они образуют невероятно сложные лабиринты. Размеры последующих лабиринтов растут экспоненциально – и их бесконечное количество», – объясняет Феликс Фликер.

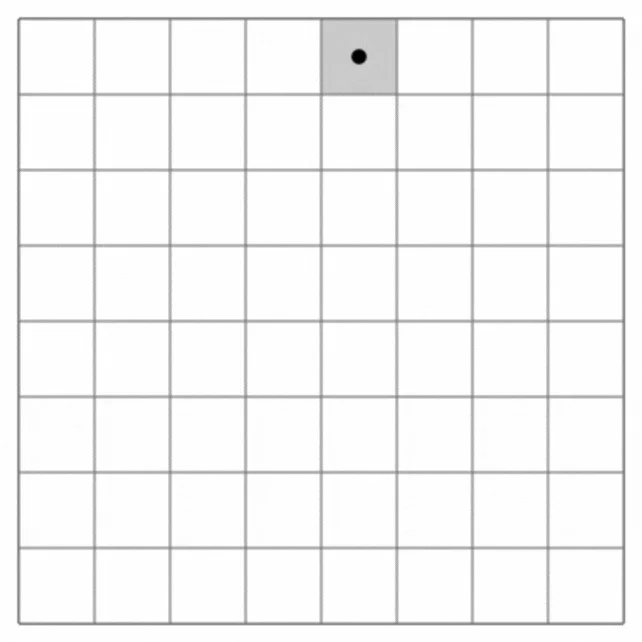
«При ходе коня шахматная фигура (которая прыгает на две клетки вперед и на одну вправо) посещает каждую клетку шахматной доски только один раз, прежде чем вернуться на исходную клетку. Это пример «гамильтонова цикла» – прохода по карте, в котором все точки остановки посещаются только один раз».

Квазикристаллы — это форма материи, встречающаяся в природе очень редко. Это своего рода странный гибрид упорядоченных и неупорядоченных кристаллов в твердых телах.

В упорядоченном кристалле – соли, алмазе или кварце – атомы расположены очень аккуратно, повторяясь в трех измерениях. Вы можете взять часть этой решетки и наложить ее на другую, и они идеально совпадут. Неупорядоченное или аморфное твердое тело — это твердое тело, в котором атомы расположены беспорядочно. К ним относятся стекло и некоторые виды льда, обычно не встречающиеся на Земле.

Квазикристалл — это материал, в котором атомы образуют узор, но узор не повторяется идеально. Они могут казаться очень похожими, но наложенные друг на друга части узора не будут совпадать.

Неидентичные шаблоны очень похожи на математическую концепцию, называемую апериодическими мозаиками, которая включает в себя шаблоны фигур, которые не повторяются одинаково. Знаменитая мозаика Пенроуза — одна из них. Еще один пример — мозаика Аммана-Бенкера.

Используя набор двумерных мозаик Аммана-Бинкера, ученые сгенерировали гамильтоновы циклы, которые, по их словам, описывают атомную структуру квазикристалла.

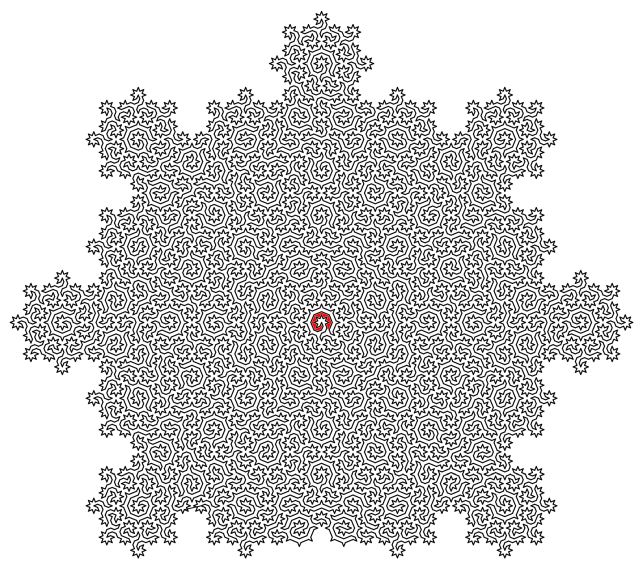
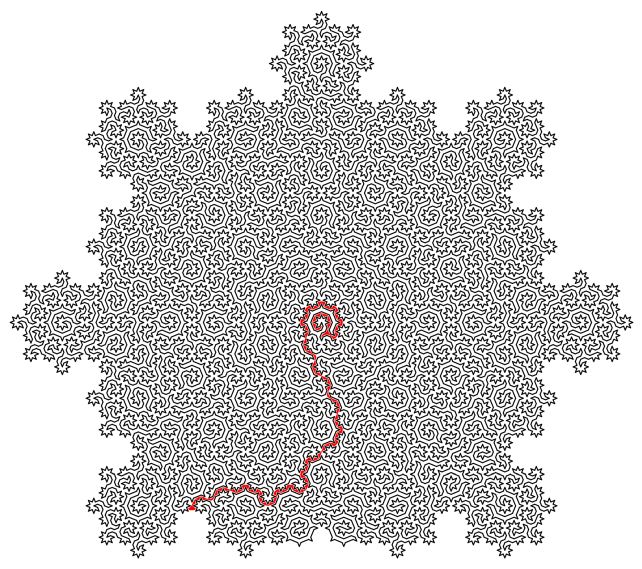
Генерируемые ими циклы посещают каждый атом квазикристалла только один раз, соединяя все атомы в единую линию, которая никогда не пересекает сама себя, но четко продолжается от начала до конца. И это можно масштабировать бесконечно, создавая математическую модель, известную как фрактал, в которой мельчайшие части напоминают самые большие.

Эта линия естественным образом создает лабиринт с начальной точкой и выходом. Но исследование имеет гораздо большее значение, чем просто развлечение.

Во-первых, найти гамильтоновы циклы чрезвычайно сложно. Решение, которое позволит идентифицировать гамильтонианы, потенциально может решить многие другие сложные математические проблемы, от сложных систем поиска маршрутов до сворачивания белков.

И, что интересно, есть последствия для улавливания углерода посредством адсорбции — промышленного процесса, который включает в себя улавливание молекул жидкости путем прилипания их к кристаллам. Если бы вместо этого можно было использовать квазикристаллы, гибкие молекулы могли бы упаковываться более плотно, располагаясь в них вдоль гамильтониана.

«Наша работа также показывает, что квазикристаллы могут быть лучше кристаллов для некоторых применений адсорбции», — говорят ученые. «Например, гибкие молекулы найдут больше способов приземлиться на неравномерно расположенные атомы квазикристаллов. Квазикристаллы также хрупкие, то есть они легко распадаются на мельчайшие зерна. Это максимизирует площадь их поверхности для адсорбции».

Исследование было опубликовано в журнале Physical Review X.