Свита королевы чисел

«Власть чисел тем могущественнее,

чем меньше в них разбираются».

Вольтер

Числа представляют собой самою могучую и закрытую империю в масштабах Вселенной. Власть в этой империи принадлежит ведущим числам. Они определяют главные принципы и правила в математических изысканиях. Пути к познанию свойств чисел будут всегда непредсказуемы. Они полностью отражают разнообразие окружающего мира и его духовное содержание. Числа могут быть мощным средством в руках человека при условии раскрытия их уникальных свойств. Они укажут путь к иным мирам и станут надёжной опорой разума человека.

Мир начинался с понятия количества, которое включало в себя неизвестное первоначальное число. Его источником был хаос. Сами числа стали формой знакового хаоса. На их построение не действуют никакие правила и нормы. Я считаю алгоритм создания их хаотичной последовательности самой главной тайной. Только в математике можно заранее определить порядок построения чисел. К их толкованию в нумерологии нужно относиться с уважением. Никто в настоящее время не знает подлинного смысла чисел и всех сфер их применения. В бесконечных последовательностях цифр заранее заложены физические и духовные свойства.

Числа не мертвы и не безучастны. Они могут реально заговорить, если подобрать ключи к их внутренним хранилищам и тайнам. Потенциал нераскрытых возможностей чисел целиком зависит от их сочетаний.

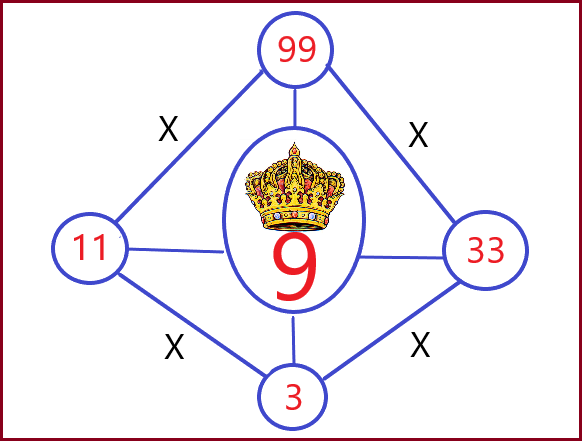
Из девяти натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9 можно выбрать самые удачные варианты действий на математическом поле. В своей статье «Королева чисел» я показал возможности девятки в математических вычислениях. Но она не одинока в системе простых решений. Особыми отношениями с ней связаны числа: 3 11, 33, 99. Их по праву можно отнести к свите королевы чисел. Они являются её ближайшими соучастниками в алгоритме многих вычислений.

Их применение значительно упрощает многие математические действия. Ведущую роль в них я отвожу числу 99. В нём умещается: 33 тройки, 11 девяток и 99 единиц. В пропорциях частей этого числа (99 — 61 — 38) присутствует золотое сечение (1,6). Но в этих частях числа скрывается не только «золото», но и квадрат 99 равный 9801. Он вычисляется так: 99 х 61 = 6039; 99 х 38 = 3762; 6039 + 3762 = 9801; 99 х 99 = 9801. Мне не известно, к чему ещё может «прикоснуться» это число, чтобы получился не менее ценный результат. Оно не единственное в окружении девятки. Её дальними «родственниками», с похожими свойствами, являются все числа, которые озаглавлены цифрой 9. К ним относятся: 91, 92, 93,94, 95, 96, 97, 98, числа от 991 до 999…, и 9(1-8)9.

Результаты, полученные с участием этих чисел, могут быть самыми неожиданными. Их внутренние качества и простые правила помогают выполнять все операции с большими числами легко и просто.

Число 99 имеет свою историю:

• В египетской мифологии оно связано с богиней Нут, которая воспламеняет души умерших. Древние египтяне считали это число богиней ночи и творцом небесных объектов.
• Башни-близнецы в Нью-Йорке, разрушенные террористами 11 сентября, являлись символом числа 99.
• В исламе верующие во время молитв применяют чётки, состоящие из 99 бусин. Имеются чётки из 33 бусин, что составляет треть от 99.
• В математике с помощью числа 3 можно превратить 99 в числа 11 и 33. В нём содержатся три шестёрки (9 + 9 =18 или 6 + 6 + 6 = 18). Делителями этого числа являются: 1,3, 9,11, 33,99. Квадратный корень из 99 равен 9, 94987.
• В числе Пи последовательность шести девяток начинается после 761 цифры после запятой. Она известна, как «точка Ричарда Фейнмана».
• В литературных произведениях, переведённых на цифровой язык, число 9 по частоте применения в текстах занимает наряду с другими знаками среднее место.

Эффективность числа 99 в математике можно доказать только с помощью практических вычислений.

Посох для чисел

В решении любых математических задач и примеров требуется опора на разработанные формулы и правила. От их применения зависят эффективность и простота вычислений. Нахождение самих правил в отношениях между различными числами является непростой задачей. Символической опорой в решении сложных задач в математике можно считать посох. Он даёт возможность управлять числами и успешно применять их скрытые свойства. Я отношу к этой опоре все формулы и правила в сфере чисел. Это необходимый принцип в математическом искусстве вычислений.

Например, в религии буддизма посох является символом знания, которое служит опорой человеку в его жизни. Правила играют роль ключа в преодолении математических преград и трудностей. Для примера возьмём самое простое умножение числа 99 на однозначные числа (от2 до 9). Представляю таблицу этих вычислений:

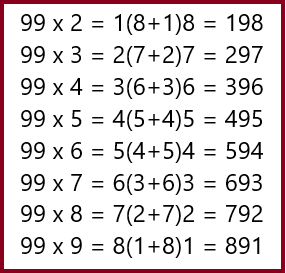
В ней каждое число дважды умножается на девятку, а средние цифры ответов превращаются в число 9. Для получения ответа нужно научиться автоматически определять крайние цифры, а между ними ставить девятку.

Следующая таблица покажет умножение числа 99 на любое двузначное число. В ней умножение чисел заменяется двумя простыми вычитаниями:

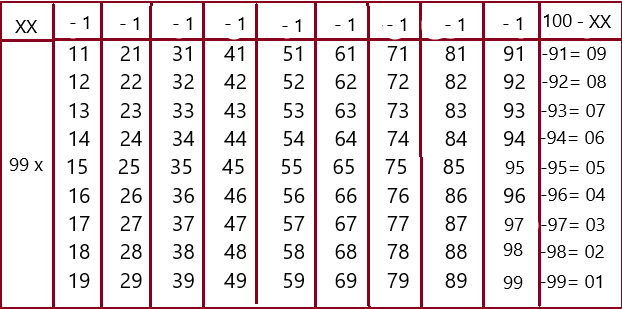
Последний столбик таблицы показывает, как нужно выполнять второе вычитание. Представляю её применение на трёх примерах:

1. 99 х 37 = 3663. Решение: 37 – 1 = 36; 100 – 37 = 63. Ответ: 3763.
2. 99 х 68 = 6732. Решение: 68 – 1 = 67; 100 – 68 = 32. Ответ: 6732.
3. 99 х 94 = 9306. Решение: 94 – 1 = 93; 100 – 94 = 06. Ответ: 9306.

Все остальные примеры таблицы решаются аналогичным способом.

Число 99 можно увеличить или уменьшить до 10 единиц. При этом его свойства в этих числах сохранятся. Они скроются внутри новых чисел:

99 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 +1 + 1;

99 – 1 – 1 – 1 – 1 – 1 – 1 – 1 – 1 – 1 – 1;

Образуются две линейки новых чисел:

100 101 102 103 104 105 106 107 108 109

98 97 96 95 94 93 92 91 90 89

Эти базисные числа можно умножать на любое двузначное число. Проверим их возможности на двух примерах из каждого ряда:

1. 106 х 43 = 4558.

Решение: (106 – 7) х 43; 99 х 43 = 4257; 7 х 43 = 301; 4257 + 301 = 4558.

1. 104 х 78 = 8112.

Решение: (104 – 5) х 78; 99 х 78 = 7722; 5 х 78 = 390; 7722 + 390 = 8112.

1. 94 х 68 = 6392.

Решение: (94 + 5) х 68; 99 х 68 = 6732; 5 х 68 = 340; 6732 – 340 = 6392.

1. 97 х 48 = 4656.

Решение: (97 + 2) х 48; 99 х 48 = 4752; 2 х 48 = 96;4752 – 96 = 4656.

Некоторые сложности возникнут, если числа из этих рядов умножить на любые трёхзначные числа. Выберем из множества вариантов два примера:

1. 107 х 354 = 37878.

Решение: (107 – 8) х 354; 99 х 350 = 34650; 99 х 4 = 396; 34650 + 396 = 35046; 8 х 354 = 2832; 35046 + 2832 = 37878.

1. 96 х 842 = 80832.

Решение: (96 + 3) х 842; 99 х 840 = 83160 – 198 = 83358;

99 х 2 = 198; 3 х 842 = 2526; 83358 – 2526 = 80832.

Должен заметить, что в решении этих примеров устно требуется определённый опыт.

Увеличим число 99 в два раза: 99 х 2 = 198.

Умножим это число на любое двузначное и определим алгоритм его решения на двух примерах:

1. 198 х 24 = 4752.

Решение: (198 : 2) х 24; 99 х 24 = (24 – 1 = 23; 100 – 24 = 76) = 2376 х 2 = 4752.

1. 198 х 76 = 15048.

Решение: (198 : 2) х 76; 99 х 76 = (76 — 1 =75; 100 – 76 = 24) =7524 х 2 = 15048.

Увеличим число 99 в девять раз: 99 х 9 = 891. Решим пример с этим числом:

891 х 94 = 83754.

Решение: (891:9) х 94; 99 х 94 = (94 – 1 = 93; 100 – 94 = 06) = 9306 х 9 = 83754.

Число 99 можно увеличить от двух до девяти раз и затем умножать на двузначное число. Все методы их решений будут одинаковыми.

Уменьшим число 99 в три раза: (99:3 = 33). Решим пример:

33 х 48 = 1584.

Решение: (33 х 3) х 48; 99 х 48 = (48 – 1 = 47; 100 – 48 = 52) = 4752 : 3 = 1584.

Разделим число 99 на 9 получим 11. Решим пример:

11 х 73 = 803.

Решение: 7 + 3 = 10; 1 + 7= 8; Ответ: 803.

Подобные примеры решаются сложением двух чисел, а результат ставится между этими цифрами.

Добавим к числу 99 ещё одну девятку и получим число 999.

Умножим число 999 на любое двузначное число. Например:

999 х 68 = 67932.

Решение: 68 – 1 = 67; 100 – 68 = 32. Ответ: 67932.

При умножении 999 на другие двузначные числа девятка всегда будет присутствовать в ответах между двумя парами чисел. Количество этих девяток в ответах будет увеличиваться при числах 9999, 99999, 999999 и при других их количествах. Например:

1. 9999 х 73 = 729927.

Решение: 73 — 1 = 72; 1000 – 73 = 927; Ответ: 729927.

1. 99999 х 56 = 5599944.

Решение: 56 — 1 = 55; 1000 – 56 = 944; Ответ: 5599944.

1. 999999 х 83 = 82999917.

Решение: 83 – 1 = 82; 1000 – 83 = 917; Ответ: 82999917.

Подобные примеры можно продолжать и дальше. Результаты будут такими же.

Исследуем умножение числа 999 на трёхзначное число. Примеры:

1. 999 х 781 = 780219.

Решение: 781 – 1 = 780; 1000 – 781 = 219; Ответ: 780219.

1. 999 х 643 = 642357.

Решение: 643 – 1 = 642; 1000 – 643 = 357; Ответ: 642357.

Если из числа 999 отнимем 9 единиц, получим очередное базисное число 990. Его можно умножать на двух и трёхзначные числа. Проверим его свойства на двух примерах:

1. 990 х 83 = 82 170.

Решение: 83 – 1 = 82; 10 х 17 = 170; Ответ: 82170.

В этом примере перемножаются числа, которые дополняют 90 и 83 до ста.

1. 990 х 584 = 578160.

Решение: 990 х (580 – 4); 990 х 580 = 574200; 4 х 990 = 3960; 574200 + 3960 = 578160.

Число 990 можно уменьшать на количество единиц от 1 до 9 и его основные свойства сохранятся. Получим ещё один перечень чисел:

989 988 987 986 985 984 983 982 981 980.

Любое из этих чисел можно умножить на двух и трёхзначные числа и получить результат. Примеры:

1. 987 х 82 = 80934.

Решение: (987 +3) х 82; 990 х 82 = 81180; 3 х 82 = 246; 81180 – 246 = 80934.

1. 988 х 248 = 245024.

Решение: (988 +2) х 248; 990 х (240 + 8); 990 х 8 = 7920;

990 Х 240 = 237600 + 7920 = 245520; 2 х 248 = 496; 245520 – 496 = 245024.

Перемножим число 9999 на трёхзначное.

Пример: 9999 х 384 = 3839616.

Решение: 384 – 1 = 383; 1000 – 384 = 616; Ответ: 3839616.

Между двумя трёхзначными числами появилась девятка. Она будет присутствовать и при всех других подобных решениях.

Завершим исследование последним примером из серии девяток.

9999 х 7684 = 76832316.

Решение: 7684 – 1 = 7683; 10000 — 7684 = 2316; Ответ: 76832316.

Могу предположить, что во всех этих вычислениях определяющую роль сыграла незаметная единица. Её не хватило для превращения 99 в сотню, 999 – в тысячу, 9999 – в десять тысяч, 99999 – в сто тысяч, 999999 – в миллион.

Как поведут себя в примерах девятки, если им навязать дополнительную нагрузку:

Если к числу 9 поочерёдно присоединять цифры от 1 до 9, то получится таблица из двух множителей с девятками во главе:

91 х (от 91 до 99);

92 х (92 – 99);

93 х (93 – 99);

94 х (94 – 99);

95 х (95 – 99);

96 х (96 – 99);

97 х (97 – 99);

98 х (98 – 99);

99 х 99.

В этой таблице присутствует 37 примеров, каждый из которых решается по двум правилам:

1. В каждом множителе нужно определить количество единиц, которых не хватает до ста. Например: числу 93 до ста не хватает 7, а числу 96 – 4.
2. Из первого множителя отнимается количество единиц, которых не хватает до ста у второго множителя. Не достающиеся единицы до ста у двух множителей перемножаются и получается общий ответ.

Проверим эти правила на трёх выбранных из таблицы примерах:

1. 94 х 96 = 9024.

Решение: 94 – 4 = 90; 6 х 4 = 24; Ответ: 9024.

1. 97 х 94 = 9118.

Решение: 97 – 6 = 91; 3 х 6 = 18; Ответ: 9118.

1. 99 х 99 = 9801.

Решение: 99 – 1 = 98; 1 х 1 = 1; Ответ: 9801.

Составим таблицу вариантов умножения трёхзначных чисел с девятками во главе:

991 х (от 991 до 999)

992 х (992 – 999);

993 х (993 – 999;

994 х (994 – 999);

995 х (995 – 999);

996 х (996 – 999);

997 х (997 – 999);

998 х (998 – 999);

999 х 999.

Решим из этой таблицы два примера (правила одинаковые):

1. 994 х 998 = 992012.

Решение: 94 – 2 = 992; 6 х 2 = 12; Ответ: 992012.

В ответах всегда будет присутствовать 0 между тремя и двумя цифрами.

1. 991 х 997 = 988027.

Решение: 91 – 3 = 988; 9 х 3 = 27; Ответ: 988027.

По таким же правилам можно умножать четырёхзначные и пятизначные числа:

1. 9996 х 9994 = 99900024.

Решение: 96 – 6 = 9990; 4 х 6 = 24; Ответ: 99900024.

1. 99998 х 99996 = 9999400008.

Решение: 98 – 4 = 99994; 2 х 4 = 8; Ответ: 9999400008.

Подобное увеличение девяток может быть бесконечным. А решение будет таким же лёгким.

Поместим дополнительные числа между девятками и решим подобные примеры:

1. 939 х 989 = 928671.

Решение: 939 – 11 = 928; 61 х 11 = 671; Ответ: 928671.

Примечание к решению этого примера: числу 939 не хватает до тысячи 61, а числу 989 – 11. 61 х 11 = 671.

1. 9949 х 9989 = 99380561.

Решение: 9949 – 11 = 9938; 51 х 11 = 561; Ответ: 99380561.

1. 9979 х 9949 =99281071.

Решение: 9979 – 51 – 9928; 21 х 51 = 1071; Ответ: 99281071.

Числа с ещё большим количеством знаков можно решить таким же способом.

Возведение чисел в квадрат

Возведение в квадрат двузначных чисел. В начале каждого числа девятка:

91 х 91 = 8281. Решение: 91 – 9 = 82; 9 х 9 = 81; ответ: 8281.

92 х 92 = 8464. Решение: 92 – 8 = 84; 8 х 8 = 64; ответ: 8464.

93 х 93 = 8649. Решение: 93 – 7 = 86; 7 х 7 = 49; ответ: 8649.

94 х 94 = 8836. Решение: 94 – 6 = 88; 6 х 6 = 36; ответ: 8836.

95 х 95 = 9025. Решение: 95 – 5 = 90; 5 х 5 = 25; ответ: 9025.

96 х 96 = 9216. Решение: 96 – 4 = 92; 4 х 4 = 16; ответ: 9216.

97 х 97 = 9409. Решение: 97 – 3 = 94; 3 х 3 = 9; ответ: 9409.

98 х 98 = 9604. Решение: 98 – 2 = 96; 2 х 2 = 4; ответ: 9604.

99 х 99 = 9801. Решение: 99 – 1 = 98; 1 х 1 = 1; ответ: 9801.

В решении умножаются числа, которых не хватает до ста.

Возведение в квадрат трёхзначных чисел, которые начинаются с двух девяток:

991 х 991 = 982081. Решение: 91 – 9 = 982; 9 х 9 = 81; ответ: 982081.

992 х 992 = 984064. Решение: 92 – 8 = 984; 8 х 8 = 64; ответ: 984064.

993 х 993 = 986049. Решение: 93 – 7 = 986; 7 х 7 = 49; ответ: 986049.

994 х 994 = 988036. Решение: 94 – 6 = 988; 6 х 6 = 36; ответ: 986036.

995 х 995 = 990025. Решение: 95 – 5 = 990; 5 х 5 = 25; ответ: 990025.

996 х 996 = 992016. Решение: 96 – 4 = 992; 4 х 4 = 16; ответ: 992016.

997 х 997 = 994009. Решение: 97 – 3 = 994; 3 х 3 = 9; ответ: 994009.

998 х 998 = 996004. Решение: 98 – 2 = 996; 2 х 2 = 4; ответ: 996004.

999 х 999 = 998001. Решение: 99 – 1 = 998; 1 х 1 = 1; ответ: 998001

Возведение в квадрат чисел, когда между двумя девятками находится одна из цифр (1-9). Примеры:

1. 939 х 939 = 881721.

Решение: 939 – 61 = 878; 61 х 61 = (3)721; 878 + 3 = 881; Ответ: 881721.

1. 979 х 979 = 958441.

Решение: 979 – 21 = 958; 21 х 21 =441; Ответ: 958441.

Примеры возведения в квадрат четырёхзначных чисел с тремя девятками:

1. 9994 х 9994 = 99880036.

Решение: 94 – 6 = 9988; 6 х 6 = 36; Ответ: 99880036.

1. 9997 х 9997 = 99940009.

Решение: 97 – 3 = 9994; 3 х 3 = 9; Ответ: 99940009.

Остальные примеры этого ряда решаются таким же способом.

Из всех приведённых выше примеров можно сделать вывод:

Числа 9 и 99 в цифровой массе имеют мощную корневую систему. У них имеются ответвления ко многим цифровым образованиям. Эти числа обладают цифровыми истинами на прочной основе правил. Их превосходство в вычислительной практике перед другими числами не вызывает сомнений.

Во всех представленных выше примерах показаны лишь некоторые приёмы упрощённого вычисления больших чисел.

Я убеждён, что любители математики найдут в царстве чисел немало других методов в решении сложных задач. Если мои исследования в этой сфере принесут какую-то практическую пользу, значит я трудился не напрасно.

Редакция не несёт ответственности за содержание предоставленного материала. Мнение авторов публикаций в разделе «Авторский материал» не обязательно отражает точку зрения редакции.