Математики решили ключевую задачу ленты Мёбиуса после почти 50 лет поисков

На протяжении почти пятидесяти лет математики ломали голову над обманчиво простым вопросом: насколько маленькой можно сделать ленту Мёбиуса, чтобы она не пересекалась сама с собой?

Теперь Ричард Шварц, математик из Университета Брауна, предложил элегантное решение этой проблемы, первоначально поставленной математиками Чарльзом Уивером и Бенджамином Халперном в 1977 году.

В своей статье Халперн и Уивер устанавливают ограничение для лент Мёбиуса, основанное на знакомой геометрии сложенных кусочков твердой бумаги: соотношение между длиной и шириной бумаги должно быть больше √3, или около 1,73.

Например, лента Мёбиуса длиной в один сантиметр должна быть шире, чем √3 или 1,73 сантиметра.

Ричард Шварц заинтересовался этим вопросом и предпринял несколько попыток решить проблему, и в 2021 году опубликовал статью с многообещающим подходом, который в конечном итоге потерпел неудачу.

Он не мог оставить эту проблему в покое и недавно начал экспериментировать со сжатием бумажных лент Мёбиуса в надежде, что двумерную форму будет легче решить математически.

Но когда он разрезал одну из этих петель под углом (что было необходимо для решения его задачи оптимизации), он увидел то, чего не ожидал.

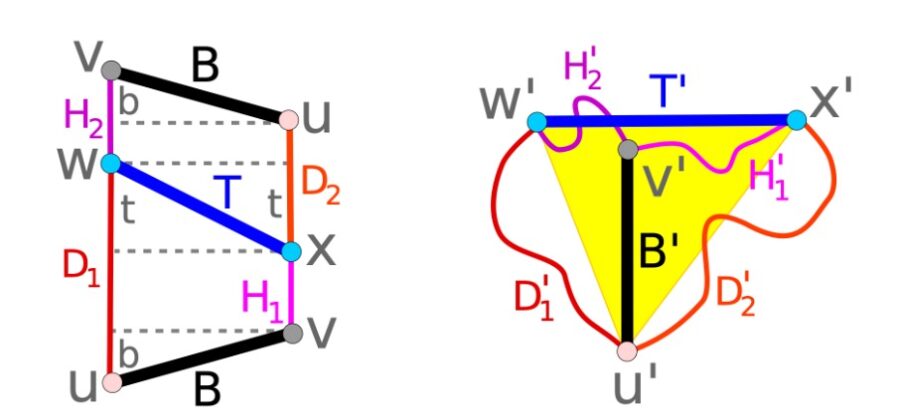
Длина двухмерного листа бумаги не была похожа на параллелограмм, как он сообщал в своей первой статье. Скорее, это была трапеция – форма с четырьмя прямыми сторонами, из которых только две стороны параллельны друг другу.

«Недавно я обнаружил, что допустил ошибку при постановке задачи оптимизации», — пишет Ричард Шварц.

За три бессонные ночи – при некоторой помощи нескольких коллег – Шварц исправил свою ошибку и нашел «действительно хорошее доказательство» промежуточного шага, «которое значительно упростило» работу.

«Я был поражен и обрадован, обнаружив, что, когда я правильно решил задачу оптимизации, я получил… √3» пишет Ричард Шварц.

Ленты Мёбиуса обладают множеством странных свойств, что сделало их объектом восхищения с тех пор, как они были описаны в 1858 году немецкими математиками Августом Мёбиусом и Иоганном Листингом.

Ленты Мёбиуса неориентируемы. Это означает, что муравей, блуждающий по ленте Мёбиуса, никогда не оказывается «внутри» или «снаружи», «верху» или «низу» фигуры.

Во время своего путешествия муравьи одним непрерывным движением охватывают обе стороны ленты.

Возможность использовать обе стороны поверхности без необходимости переворачивать ленту сделала ленты Мёбиуса полезными для магнитофонов, пишущих машинок, конвейерных лент, картриджей для печати и американских горок.

Ленты Мёбиуса используются в ювелирных изделиях, международном символе переработки и в логотипе Google Drive, поскольку они представляют собой бесконечные петли.

Статья опубликована на сайте препринтов ArXiv.