Геометрическая топология: изучение пространств и их форм

Геометрическая топология — это область математики, которая изучает свойства пространств и их форм, а также то, как эти пространства могут быть вложены друг в друга. Она играет ключевую роль в понимании не только нашей планеты и Вселенной, но и в решении множества практических задач, начиная от проектирования роботов и заканчивая анализом больших данных. В основе топологии лежит идея о том, что пространства могут иметь различную форму и структуру, и эти свойства влияют на то, как мы воспринимаем и взаимодействуем с миром.

Двумерные пространства: от плоской Земли до поверхности пончика

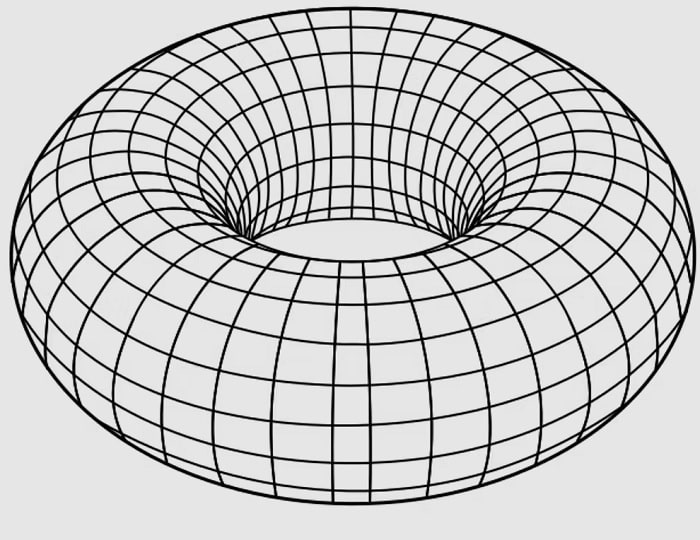
Когда мы смотрим на окружающий мир, он кажется плоским, особенно если рассматривать его в локальном масштабе. Например, карта города — это плоское представление местности, которое помогает нам ориентироваться. Однако в глобальном масштабе Земля — это не плоскость, а сфера. Поверхность Земли — это пример двумерного пространства, где можно двигаться в двух направлениях: на север-юг и на восток-запад. Но сфера — не единственное возможное двумерное пространство. Другим примером является поверхность тора, или пончика. В отличие от сферы, тор имеет «дырку» в центре, что придает ему уникальные топологические свойства.

Математики уже более века изучают все возможные двумерные пространства и их свойства. Эти знания помогают не только в теоретических исследованиях, но и в практических приложениях, таких как проектирование спутников или анализ данных.

Трехмерные пространства: форма Вселенной

Если двумерные пространства, такие как поверхность Земли, можно представить относительно легко, то трехмерные пространства, в которых мы живем, гораздо сложнее. Вселенная, которую мы наблюдаем, кажется трехмерной: мы можем двигаться вверх-вниз, влево-вправо и вперед-назад. Однако, как и в случае с Землей, глобальная структура Вселенной может быть более сложной. Возможно, она представляет собой трехмерный аналог поверхности сферы или тора, или даже что-то более экзотическое.

За последние несколько десятилетий математики значительно продвинулись в понимании трехмерных пространств. Хотя полная классификация таких пространств еще не завершена, уже известно множество их свойств. Эти знания помогают физикам и астрономам в попытках определить, в каком именно трехмерном пространстве мы живем. Вопрос о форме Вселенной остается открытым, но топология предоставляет инструменты для его изучения.

Четырехмерные пространства: время как измерение

Когда мы добавляем время к трем пространственным измерениям, мы получаем четырехмерное пространство-время. Например, чтобы описать положение кометы, нужно указать три координаты для ее местоположения и одну — для момента времени. Такое четырехмерное пространство может иметь сложную структуру, и его изучение является важной частью современной физики и математики.

Теория струн, например, предполагает, что Вселенная может иметь больше измерений, чем четыре. Эти дополнительные измерения могут быть компактифицированы, то есть свернуты в очень маленькие масштабы, что делает их ненаблюдаемыми в повседневной жизни. Изучение многомерных пространств важно не только для фундаментальной науки, но и для практических приложений, таких как планирование движения роботов или моделирование сложных систем.

Многомерные пространства: от роботов до больших данных

Многомерные пространства возникают во множестве научных и инженерных задач. Например, если рассматривать движение нескольких роботов в помещении, то положение каждого робота можно описать двумя координатами (x и y). Для трех роботов потребуется уже шесть координат, что соответствует шестимерному пространству. Если добавить информацию о препятствиях или других параметрах, размерность пространства увеличивается еще больше.

Аналогично, в анализе больших данных каждая точка данных может быть представлена как вектор в многомерном пространстве. Понимание структуры таких пространств помогает в обработке и интерпретации данных. Топология предоставляет методы для изучения этих сложных структур, что делает ее незаменимым инструментом в современной науке и технике.

Узлы и вложения пространств

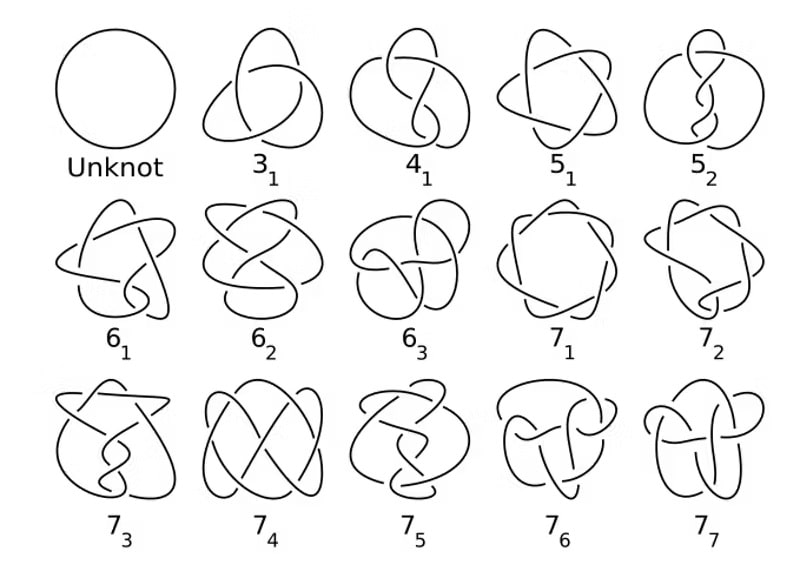
Топология также изучает, как одно пространство может быть вложено в другое. Например, узел на веревке — это одномерное пространство (петля), вложенное в трехмерное пространство (комната). Математические узлы имеют важное значение для понимания трехмерных и четырехмерных пространств. Они используются в различных областях, от физики (теория струн) до биологии (рекомбинация ДНК) и химии (хиральность молекул).

Изучение узлов — это не только теоретическая задача, но и практическая. Например, понимание того, как узлы ведут себя в трехмерном и четырехмерном пространствах, может помочь в разработке новых материалов или в моделировании биологических процессов.

Открытые вопросы и будущее топологии

Геометрическая топология продолжает развиваться, и перед исследователями стоит множество нерешенных задач. Одной из таких задач является гипотеза Пуанкаре о гладком четырехмерном пространстве, которая пытается определить, что такое «простейшее» замкнутое четырехмерное пространство. Другой важной проблемой является гипотеза о срезанной ленте, которая связывает узлы в трехмерных пространствах с поверхностями в четырехмерных.

Топология уже находит применение в науке и технике, и дальнейшее развитие этой области будет иметь огромное значение для понимания мира, в котором мы живем. Раскрытие тайн пространств во всех измерениях поможет не только углубить наши знания о Вселенной, но и решить множество практических задач, от проектирования роботов до анализа сложных данных.